Un blog con cuestiones, ejercicios, problemas, aplicaciones y comentarios relacionados con los contenidos de Matemáticas del cuarto curso de ESO
miércoles, 21 de diciembre de 2016
Ejercicios resueltos y comentados del examen de sistemas de ecuaciones, realizado el viernes 16/12/2016
Resolviendo problemas de geometría mediante el álgebra
SOLUCIÓN.
Resolución de problemas aritméticos mediante el álgebra
SOLUCIÓN.
lunes, 19 de diciembre de 2016
Resolviendo un sistema de ecuaciones no lineales
SOLUCIÓN.
En general, para resolver un sistema de ecuaciones no lineales no sirve el método de reducción; sin embargo, hay excepciones: este sistema, por ejemplo, sí podemos resolverlo por dicho método, y de una forma muy sencilla:
Sumando la primera y la segunda ecuaciones, miembro a miembro, obtenemos una nueva ecuación equivalente, $2x^2=8$, que nos permite escribir el siguiente sistema equivalente:
$$\left\{\begin{matrix}x^2 & - & y^2 & = & 4 \\ 2\,x^2 & & & = & 8 \end{matrix}\right. $$ Así, de la nueva segunda ecuación deducimos $$x^2=4 \Leftrightarrow x=\pm 2$$ Y sustituyendo $x^2=4$ en, por ejemplo, la primera, $$y^2=0 \Leftrightarrow y=0$$ De donde concluimos que $$\begin{matrix}\text{si} & x=-2 & \text{entonces} & y=0 \\ \\ \text{si} & x=+2 & \text{entonces} & y=0\end{matrix}$$
$\square$
Resolviendo un sistema de ecuaciones lineales
SOLUCIÓN.
Multiplicando por el mínimo común múltiplo de los denominadores en las respectivas ecuaciones, llegaremos a un sistema equivalente con coeficientes enteros:
$\left\{\begin{matrix}\dfrac{3}{2}\,x & - & \dfrac{2}{3}\,y & = & \dfrac{5}{12} \\ \\ \dfrac{1}{5}\,x & - & \dfrac{3}{10}\,y & = & \dfrac{1}{4}\end{matrix}\right. \overset{e_1\cdot \text{m.c.m}(2,3,12)\rightarrow e_1\quad;\quad e_2\cdot \text{m.c.m}(5,10,4)\rightarrow e_2}{\sim}$
$\sim \left\{\begin{matrix}12\cdot \dfrac{3}{2}\,x & - & 12\cdot \dfrac{2}{3}\,y & = & 12\cdot \dfrac{5}{12} \\ \\ 20\cdot\dfrac{1}{5}\,x & - & 20\cdot \dfrac{3}{10}\,y & = & 20\cdot \dfrac{1}{4}\end{matrix}\right. \sim $
Procedemos ahora a reducir el sistema mediante la operación elemental que se indica:
$ \sim \left\{\begin{matrix}6\cdot 3\,x & - & 4\cdot 2 \,y & = & 5 \\ \\ 4\,x & - & 2\cdot 3 \,y & = & 5\end{matrix}\right. \sim \left\{\begin{matrix}18\,x & - & 8\,y & = & 5 \\ \\ 4\,x & - & 6\,y & = & 5\end{matrix}\right. \overset{-2\,e_1+9\,e_2 \;\rightarrow\; e_2}{\sim} $
$ \sim \left\{\begin{matrix}18\,x & - & 8\,y & = & 5 \\ \\ & - & 38\,y & = & 35\end{matrix}\right. \sim \left\{\begin{matrix}18\,x & - & 8\cdot (-\dfrac{35}{38}) & = & 5 \\ \\ & & y & = & -\dfrac{35}{38}\end{matrix}\right. \sim $
$\sim \left\{\begin{matrix}x & & & = & -\dfrac{5}{38} \\ \\ & & y & = & -\dfrac{35}{38}\end{matrix}\right.$
$\square$
jueves, 15 de diciembre de 2016
Otro problema de combinatoria ordenando letras
SOLUCIÓN.
Tengamos en cuenta que:
1. Pensando en el grupo de cuatro caracteres ( dos consonantes y dos vocales ), y reparando en el requerimiento ( del enunciado ) que las vocales no puedan estar juntas, debemos entender que hay que restar de las $\text{P}_4=4!$ posibilidades ( sin esa restricción ) las que corresponden a estar éstas juntas las dos vocales, esto es, $\text{P}_3\cdot 2!$ ( donde consideramos el bloque de las dos vocales como un sólo símbolo y tenemos en cuenta que esas dos vocales se permutan la una con la otra ); por consiguiente tenemos $4!- 3!\cdot 2=12$ posibilidades
2. En relación a las dos consonantes que deben tener dichas palabras, hay $\displaystyle \binom{4}{2}$ maneras de elegirlas
Así pues, de (1) y (2), por el principio multiplicativo, tenemos $\displaystyle 12 \cdot \binom{4}{2}=72$ palabras con las condiciones pedidas.
$\square$
Formando 'palabras'
SOLUCIÓN.
Tengamos en cuenta que:
1. Hay $4!$ posibilidades al permutar las cuatro letras de la palabra que queremos formar
2. En relación a las dos consonantes que deben tener dichas palabras, hay $\displaystyle \binom{4}{2}$ maneras de elegirlas
Así pues, de (1) y (2), por el principio multiplicativo, tenemos $\displaystyle 4!\cdot \binom{4}{2}=144$ palabras con las condiciones pedidas.
$\square$
Permutaciones
SOLUCIÓN. Considerando el conjunto $\{\text{B},\text{A},\text{R}\}$ como un sólo caracter/símbolo, debemos permutar los $6$ caracteres/símbolos siguientes: el bloque $\{\text{B},\text{A},\text{R}\}$, el símbolo Í, el símbolo $\text{T}$, el símbolo $\text{N}$, y las dos $\text{O}$s; así que, teniendo en cuenta que la $\text{O}$ aparece dos veces, obtenemos $$\dfrac{6!}{2!}\; \text{posibilidades}$$ Por otra parte, las letras del grupo $\{\text{B},\text{A},\text{R}\}$ pueden a su vez permutarse entre sí de $3!$ maneras distintas; por tanto, tendremos un total de $$\dfrac{3! \cdot 6!}{2!}=2160\;\text{palabras}$$
$\square$
martes, 13 de diciembre de 2016
Resolviendo ecuaciones con términos logarítmicos
SOLUCIÓN. Aplicando las propiedades de los logaritmos en el primer miembro llegamos a $$\log\,(x\cdot x^2)=3$$ y por tanto $$\log\,x^3=3$$ con lo cual $$3\,\log\,x=3$$ es decir $$\log\,x=1$$ y siendo $10$ la base del logaritmo, $$x= 10^1=10$$
$\square$
Resolviendo ecuaciones con términos exponenciales
SOLUCIÓN. Podemos expresar la ecuación de la forma $$2^x-2^{1-x}+1=0$$ que es equivalente a $$2^x-2\cdot 2^{-x}+1=0$$ Denotando $2^x$ por $t$, transformamos la ecuación equivalente con términos exponenciales en una ecuación con términos racionales y polinómicos $$t-\dfrac{2}{t}+1=0$$ Multiplicando ambos miembros por $t$, la trasformamos en una ecuación equivalente con términos polinómicos y de segundo grado $$t^2+t-2=0$$ cuya solución viene dada por $$t=\dfrac{-1\pm\sqrt{1^2-4\cdot 1\cdot (-2)}}{2\cdot 1}=\dfrac{-1\pm 3}{2}=\left\{\begin{matrix}1\\\\-2\end{matrix}\right.$$ Entonces, si $t=1$, se tiene que $2^x=1$, esto es, $2^x=2^0$, luego $x=0$; y, por otra parte, si $t=-2$, podemos escribir que $2^x=-2$, pero para este caso no existe ningún valor de $x$ que satisfaga la igualdad. Por tanto, la solución de la ecuación pedida viene dada por un sólo valor, que es $x=0$.
$\square$
lunes, 5 de diciembre de 2016
Ejercicios resueltos del examen de los temas 3 y 4 de 4.º de ESO, realizado el martes 29/11/2016
Factorizando polinomios
SOLUCIÓN. Hay una fórmula para encontrar las raíces de los polinomios de tercer grado, pero como se ha comentado en clase, no la usamos, por su complejidad. Como alternativa, trataremos de buscar, primero, las raíces enteras ( si las hubiera ).
Sabemos ( por un teorema enunciado en clase ) que toda raíz entera de $P(x)$ ha de ser divisor del término independiente, que en la ecuación pedida es $-2$. Como $$\text{div}(-2)=\{-2,-1,1,2\}$$ veremos a continuación si alguno de esos números cumple la condición para que sea raíz del polinomio dado, que, como sabemos es la de anular el polinomio cuando $x$ toma dicho valor.
Observemos que $P(1)=1^3+2\cdot 1^2-1-2=0$, luego $r_1=1$ es una raíz de $P(x)$, así que, por el teorema del factor, podemos escribir $$P(x)=(x-r_1)\cdot Q(x)$$ siendo $Q(x)$ el polinomio que resulta de $P(x) \div (x-1)$. Calculemos dicho polinomio.
$$\begin{array}{r|rrrr}
& 1 & 2 & -1 & -2 \\
1 & & -1 & 0 & -1 \\
\hline & 1 & 3 & 2 & 0 \end{array}$$ luego $Q(x)=x^2+3\,x+2$.
Entonces, las restantes raíces de $P(x)$ ( si las hubiera ), también han de ser raíces de $Q(x)$. Así, que vamos a calcular las raíces de $Q(x)$, esto es $\{x\in \mathbb{x}:Q(x)=0\}$ $$x^2+3\,x+2=0\Leftrightarrow x=\dfrac{-3\pm \sqrt{3^3-4\cdot 1 \cdot2}}{2\cdot 1}=\dfrac{-3\pm 1}{2}=\left\{\begin{matrix}-1 \\ \\ -2\end{matrix}\right.$$ por lo tanto, $P(x)$ tiene dos raíces más ( además de $r_1=1$, con multiplicidad igual a $1$ ), que son $r_2=-1$ y $r_2=-2$; ambas, con multiplicidad $1$, ya que al ser el polinomio $P(x)$ de grado $3$, la suma de las multiplicidades de las raíces encontradas ha de ser, a lo sumo, $3$.
Así, pues, por el teorema del factor, podemos escribir la forma factorizada de $P(x)$ pedida como $$P(x)=(x-1)(x-(-1))(x-(-2))$$ esto es $$P(x)=(x-1)(x+1)(x+2)$$
$\square$
Calculando las raíces de un polinomio
SOLUCIÓN. Extrayendo factor común de $x$, llegamos a $$x\,(x^3+x^2+x+1)$$ esto es $$(x-0)\,(x^3+x^2+x+1)$$ por lo que ( teorema del factor ) una de las raíces de $P(x)$ es $r_1=0$, con multiplicidad $m_1=1$. Si el polinomio tiene más raíces, éstas deberán ser, también, raíces de $Q(x):=x^3+x^2+x+1$. Averiguaremos ahora si este polinomio tiene raíces.
Si $Q(x)$ tiene raíces enteras, éstas han de ser divisores del término independiente, que es $1$, luego las posibles raíces enteras son $\{-1,1\}$.
Veamos si alguna de ellas lo es. Como todos los términos de $Q(x)$ son positivos, $1$ no puede ser una raíz, pues no puede anular el polinomio. Por otra parte, el valor de $Q(x)$ en $x=-1$ es $Q(x)=(-1)^3+(-1)^2+(-1)+1=0$, luego $r_2=-1$ es raíz de $Q(x)$ y, por tanto, también lo es de $P(x)$.
Dividiendo ahora $Q(x)$ entre $x-(-1)$ ( teorema del factor ), encontramos el polinomio que multiplicado por $x-(-1)$ es igual a $Q(x)$ $$\begin{array}{r|rrrr}
& 1 & 1 & 1 & 1 \\
-1 & & -1 & 0 & -1 \\
\hline & 1 & 0 & 1 & 0 \end{array}$$ Dicho polinomio es $x^2+1$, que no tiene raíces ( es un polinomio primo ), ya que, imponiendo la condición para encontrar raíces, $x^2+1=0$, vemos que $x=\sqrt{-1} \notin \mathbb{R}$
Así pues las raíces de $P(x)$ son $\{0,-1\}$, ambas con multiplicidad $1$.
$\square$
Resolviendo ecuaciones con términos exponenciales
SOLUCIÓN. La ecuación pedida tiene un término exponencial, luego podemos resolverla extrayendo logaritmos en ambos miembros, con lo que la transformaremos en una ecuación polinómica.
$4^x=3$
$\ln\,4^x=\ln\,3$
$x\,\ln\,4=\ln\,3$ ( por las propiedades de los logaritmos )
y despejando $x$ y aproximando el resultado,
$x=\dfrac{\ln\,3}{\ln\,4}\approx 0,7925$
$\square$
Resolviendo ecuaciones cuyos términos son fracciones algebraicas
SOLUCIÓN. La ecuación pedida tiene términos del tipo fracción algebraico, por lo que reduciremos dicha ecuación a una e. polinómica multiplicando los dos miembros por el mínimo común múltiplo de los polinomios de los denominadores de los términos de la ecuación.
Los polinomios $x-3$ y $x+3$ son primos, mientras que el polinomio $x^2 -9$, que es lo mismo que $x^2-3^2$ se factoriza (fácilmente), obteniéndose $x^2-9=(x-3)(x+3)$. Así, pues, por la regla de los factores, tenemos que $$\text{m.c.m}(x-3,x+3,x^2-9)=(x-3)(x+3)$$
Multiplicando en los dos miembros de la ecuación original por el mínimo común múltiplo, llegamos a $$(x-3)(x+3)\cdot \dfrac{1}{x-3}+(x-3)(x+3)\cdot\dfrac{2}{x+3}=(x-3)(x+3)\cdot\dfrac{x}{(x-3)(x+3)}$$ y simplificando se obtiene la ecuación polinómica $$x+3+2(x-3)=1$$ esto es $$x+3+2x-6=1$$ y por tanto $$3x=4$$ con lo cual $$x=\dfrac{4}{3}$$
$\square$
Resolviendo ecuaciones bicuadradas
SOLUCIÓN. La ecuación pedida es bicuadrada, ya que
podemos escribirla de la forma $$(x^2)^2-5x^2+4=0$$
y, por tanto, podemos transformarla en una ecuación cuadrática realizando el cambio $$t=x^2$$, con lo que nos queda $$t^2-5t+4=0 \Leftrightarrow t=\dfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot 1 \cdot 4}}{2\cdot 1}=\dfrac{5\pm 3}{2}=\left\{\begin{matrix}4\\ \\1\end{matrix}\right.$$ Procedemos ahora a deshacer la transformación realizada. Como $t=x^2$, entonces $x=\sqrt{t}$. Y, por consiguiente, tenemos que de $t=4$ se desprende que $x=\sqrt{4}=\left\{\begin{matrix}-2 \\ \\2\end{matrix}\right.$; y, si $t=1$, $x=\sqrt{1}=\left\{\begin{matrix}-1 \\ \\1\end{matrix}\right.$
Por lo tanto, la solución viene dada por el conjunto $$\{-2,-1,1,2\}$$
$\square$
Resolviendo ecuaciones con radicales
$$x-6=\sqrt{x+31}-7$$
SOLUCIÓN.
La ecuación pedida tiene un término radical. El índice de dicho radical es $2$ ( raíz cuadrada ), así que, después de arreglar la ecuación pedida de modo que en el segundo miembro sólo esté dicho radical, elevaremos al cuadrado en ambos miembros, al objeto de obtener una ecuación polinómica equivalente.
$x-6=\sqrt{x+31}-7$
$x-6+7=\sqrt{x+31}$
$x+1=\sqrt{x+31}$
$(x+1)^2=(\sqrt{x+31})^2$
$x^2+2x+1=x+31$
$x^2+2x+1-x-31=0$
$x^2+x-30=0 \Leftrightarrow x=\dfrac{-1\pm \sqrt{1^2-4\cdot 1 \cdot (-30)}}{2\cdot 1}=\dfrac{-1\pm 11}{2}=\left\{\begin{matrix}-6\\\\5\end{matrix}\right.$
$\square$
martes, 22 de noviembre de 2016
Ecuaciones no polinómicas
SOLUCIÓN. Tomando logaritmos en cada miembro, $$\ln\,x^x=\ln\,x^2$$ y por las propiedades de los logaritmos podemos escribir $$x\,\ln\,x=2\,\ln\,x$$ agrupando en un sólo miembro $$(x-2)\ln\,x=0\Leftrightarrow \left\{\begin{matrix}\ln\,x=0 \Leftrightarrow x=1 \\ \\ x-2=0 \Leftrightarrow x=2\end{matrix}\right.$$
Así, pues, la solución de la ecuación pedida viene dada por el conjunto $\{1,2\}$
$\square$
Ecuaciones cuyos términos son fracciones algebraicas
SOLUCIÓN. Multiplicando los dos miembros de la ecuación por el mínimo común múltiplo de los polinomios de los denominadores de las fracciones algebraicas obtendremos una ecuación equivalente, más sencilla ( una ecuación polinómica ).
Los polinomio $x-1$ y $x+1$ son primos, y el polinomio $x^2-1=x^2-1^2$ factoriza como $(x-1)(x+1)$ ( por la identidad notable ). Entonces $$\text{m.c.m}(x-1,x+1,(x-1)(x+1))=(x-1)(x+1)$$
Multiplicando pues la ecuación original por dicho mínimo común múltiplo, $$(x-1)(x+1)\,\dfrac{x}{x-1}+(x-1)(x+1)\,\dfrac{2}{x+1}=(x-1)(x+1)\,\dfrac{3}{(x-1)(x+1)}$$ simplificando $$x(x+1)+2(x-1)=3$$ esto es $$x^2+x+2x-2=3$$ y por tanto $$x^2+3x-5=0\Leftrightarrow x=\dfrac{-3\pm\sqrt{3^2-4\cdot(-5)\cdot 2}}{2\cdot 1}=\dfrac{-3\pm 7}{2}=\left\{\begin{matrix}2 \\ \\ -5\end{matrix}\right.$$
La solución de la ecuación pedida viene pues dada por el conjunto $\{-5,2\}$
$\square$
lunes, 21 de noviembre de 2016
Resolviendo ecuaciones con logaritmos
SOLUCIÓN.
$2^{2^x}=3$
$\ln\,2^{2^x}=\ln\,3$
$(2^x)\cdot\ln\,2=\ln\,3$
$(2^x)=\dfrac{\ln\,3}{\ln\,2}$
$\ln\,2^x=\ln\,(\dfrac{\ln\,3}{\ln\,2})$
$x\,\ln\,2=\ln\,\left(\dfrac{\ln\,3}{\ln\,2}\right)$
$x=\dfrac{\ln\,\left(\dfrac{\ln\,3}{\ln\,2}\right)}{\ln\,2} \approx 0,6644$
$\square$
Resolviendo ecuaciones con términos exponenciales
SOLUCIÓN.
$$2^{2^x}=2 \Leftrightarrow 2^x=1$$ y como $1$ puede expresarse como $2^0$ se tiene que $$2^x=2^0 \Leftrightarrow x=0$$
$\square$
Resolviendo ecuaciones bicuadradas
SOLUCIÓN. A pesar de que el polinomio del primer miembro es de grado $4$, sus términos tienen grados respectivos $4$, $2$ y $0$; y siendo el segundo miembro cero, la ecuación se conoce con el nombre de bicuadrada -- ya que puede expresarse de la siguiente forma $$(x^2)^2-13\,x^2+36=0$$ -- con lo que mediante la transformación $t=x^2$, llegamos a una ecuación cuadrática ( en la variable $t$ ) que sí sabemos resolver. Después de resolverla, y a partir de los valores obtenidos para $t$, tendremos que deshacer la transformación para calcular los valores de $x$ que son solución de la ecuación original.
Así, pues, tenemos que $$t^2-13t+36=0\Leftrightarrow t=\dfrac{-(-13)\pm \sqrt{(-13)^2-4\cdot 1 \cdot 36}}{2\cdot 1}=\sqrt{13 \pm 5}{2}=\left\{\begin{matrix}4\\\\9\end{matrix}\right.$$ Entonces, deshaciendo la transformación, $x=\sqrt{t}$; con lo cual, si $t=4$, $x=\sqrt{4}=\pm 2$. Y si $t=9$, $x=\sqrt{9}=\pm 3$. Por consiguiente, la solución de la ecuación pedida viene dada por el conjunto de valores $$\{-3,-2,2,3\}$$
$\square$
Resolviendo ecuaciones bicuadradas
SOLUCIÓN. A pesar de la dificultad que pueda suponer el tener que resolver una ecuación con un polinomio de grado $4$ en el primer miembro y cero en el segundo miembro, sus términos de dicho polinomio tienen grados respectivos $4$, $2$ y $0$ ( la ecuación se conoce con el nombre de bicuadrada ) y el proceso de resolución se torna bastante sencillo tal y como vamos a ver enseguida. En efecto, la ecuación puede expresarse de la siguiente forma $$(x^2)^2-13\,x^2+36=0$$, por lo que, mediante la transformación $t=x^2$, llegamos a una ecuación cuadrática ( en la variable $t$ ) que sí sabemos resolver. Después de resolverla, y a partir de los valores obtenidos para $t$, tendremos que deshacer la transformación para calcular los valores de $x$ que son solución de la ecuación original.
Así, pues, tenemos que $$t^2-13t+36=0\Leftrightarrow t=\dfrac{-(-13)\pm \sqrt{(-13)^2-4\cdot 1 \cdot 36}}{2\cdot 1}=\dfrac{13\pm 5}{2}=\left\{\begin{matrix}9\\\\ 4\end{matrix}\right.$$ Procedemos ahora a deshacer el cambio $t=x^2$. Si $t=9$, entonces $x=\sqrt{9}=\pm 3$; y, si $t=4$, entonces $x=\sqrt{4}=\pm 2$.
Concluimos pues que la solución de la ecuación pedida viene dada por el siguiente conjunto de valores $\{-4,-2,2,4\}$
$\square$
Resolviendo ecuaciones logarítmicas
SOLUCIÓN.
$3\log\,x=\log\,100+\log\,x$
$3\log\,x-\log\,x=\log\,100$
$\log\,x^3-\log\,x=\log\,100$
$\log\,\left(\dfrac{x^3}{x}\right)=\log\,100$
$\log\,x^2=\log\,100 \Leftrightarrow x^2=100 \Leftrightarrow x=\pm 10$
Ahora bien, $x=-10$ debe descartarse como solución de la ecuación original, pues $\log\,(-10)$ no está definido; por tanto, la solución a la ecuación pedida es $x=+10$
$\square$
Dividiendo polinomios
SOLUCIÓN.
Debemos tener en cuenta el teorema de la división euclídea. Sea $M(x)$ el polinomio dividendo y $N(x)$ el p. divisor, tales que $\text{grado}(M(x))\ge\text{grado}(N(x)$; $Q(x)$ el p. cociente, y $R(x)$ el p. resto. Entonces deberá cumplirse
1. $M(x)=N(x)\cdot Q(x)+R(x)$
2. $\text{grado}(R(x))\prec \text{grado}(N(x))$
Vamos a organizar los cálculos en la siguiente tabla:
dividendo divisor cociente dividendo-divisor·cociente --------- ------- -------- -------------------------- 2x^5+1 x^2-1 x^3 (2x^5+1)-(x^2-1)·x^3=2x^3+1 2x^3+1 x^2-1 2x^3+2x 2x+1 (grado(2x+1) menor que grado(x^2-1) -> fin )obteniendo, $$Q(x)=2x^3+2x$$ y $$R(x)=2x+1$$
$\square$
domingo, 20 de noviembre de 2016
Ecuaciones con términos exponenciales
SOLUCIÓN. Éste es el plan: Transformaremos la ecuación pedida en una ecuación con términos polinómicos y la resolveremos; finalmente, desharemos la transformación.
$2^{2x}-4\cdot 2^x+4=0$
$=(2^{x})^2-4\cdot 2^x+4=0$
$\overset{\text{transformación:}\; t=2^x}{=}\quad t^2-4\cdot t+4=0\Leftrightarrow (t-2)^2=0 \Leftrightarrow t=2$
Deshaciendo ahora la transformación $t=2^x$ tenemos que $$2=2^x \Leftrightarrow x=1$$
$\square$
Un ejercicio de resolución de ecuaciones con radicales
SOLUCIÓN. La ecuación tiene un término irracional, pero podemos transformarla en una ecuación polinómica:
$\sqrt{x}+2=x$
$\sqrt{x}=x-2$
$\left(x^{\frac{1}{2}}\right)^2=(x-2)^2$
$x^{\frac{1}{2}\cdot 2}=(x-2)^2$
$x^{\frac{2}{2}}=(x-2)^2$
$x^{1}=(x-2)^2$
$x=(x-2)^2$
$x=x^2-4x+4$
$0=x^2-5x+4 \Leftrightarrow x=\dfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot \cdot 4}}{2\cdot 1}=\dfrac{5\pm 3}{2}=\left\{\begin{matrix}4\\\\1\end{matrix}\right.$
$\square$
jueves, 17 de noviembre de 2016
Suma de fracciones algebraicas
SOLUCIÓN. Para efectuar esta suma de estas fracciones, $\dfrac{x}{x^2-1}$ y $\dfrac{1}{x-1}$, debemos reducirlas a común denominador, y, para ello, calcularemos el mínimo común múltiplo de los polinomios de los denominadores -- hacemos algo análogo cuando sumamos fracciones numéricas --; así que, primero, es necesario descomponer dichos polinomios en factores ( polinómicos ) primos.
Para descomponerlos, hay que calcular sus raíces. Las raíces de $x^2-1$ son $-1$ y $1$, ya que $x^2-1=0 \Leftrightarrow x \in \{-1,+1\}$, luego por el teorema del factor, podemos escribir $x^2-1=(x-1)(x+1)$. Por otra parte, el polinomio del denominador de la segunda fracción, $x-1$, es primo ( no admite descomposición ). Hecho ésto, por la regla de los factores, sabemos que el polinomio mínimo común múltiplo es el producto de los factores de base común y no común ( a cada una de las descomposiciones ), tomando de cada uno de ellos el exponente máximo ( igual que hacemos con los números enteros ). Por todo ello, $$\text{m.c.m.}(x^2-1,x-1)=\text{m.c.m.}\left((x-1)(x+1),x-1\right)=(x-1)(x+1)=x^2-1$$
Reduciendo pues las fracciones a común denominador tenemos que la primera fracción, $\dfrac{x}{x^2-1}$ no requiere ninguna transformación, pues su denominador es el propio mínimo común múltiplo. Y la segunda fracción $\dfrac{1}{x-1}$, es equivalente a $\dfrac{(x+1)}{(x-1)(x+1)}$, esto es, es equivalente a $\dfrac{(x+1)}{x^2-1}$.
Ahora ya podemos proceder a realizar la suma,
$\dfrac{x}{x^2-1}+\dfrac{1}{x-1}=$
$=\dfrac{x}{x^2-1}+\dfrac{x+1}{x^2-1}$
$=\dfrac{x+(x+1)}{x^-1}$
$=\dfrac{2x+1}{x^-1}$
y hemos terminado.
$\square$
Encontrar las raíces del polinomio y factorizarlo
a) Encontrar sus raíces
b) Factorizar el polinomio dado
SOLUCIÓN.
Por definición, el conjunto de raíces viene dado por $$\{x\in \mathbb{R}: P(x)=0\}$$ Para encontrarlas ( si tuviera ), imponemos pues la condición $$x^4+2\,x^3+2\,x^2+2\,x+1=0$$ por lo que deberemos resolver esta ecuación. Empezaremos buscando posibles raíces enteras. Sabemos ( propiedad explicada en clase ) que las posibles raíces enteras son los divisores del término independiente, que es $1$, esto es $\{-1,+1\}$. Ensayemos estos números: $$P(-1)=(+1)^4+2\cdot(+1)^3+2\cdot(+1)^2+2\cdot (+1)+1 \neq 0 \Leftrightarrow +1 \; \text{no es raíz de}\, P(x)$$ sin embargo, $-1$, sí es raíz de $P(x)$, como vamos a ver a continuación
$$P(-1)=(-1)^4+2\cdot(-1)^3+2\cdot(-1)^2+2\cdot (-1)+1=0 \Rightarrow r_1=-1$$ así que, por el teorema del factor, $(x-(-1))$, esto es $x+1$, es un polinomio primo de la descomposición ( en factores ) de $P(x)$. El polinomio que multiplicado por $x+1$ es igual a $P(x)$ se obtiene haciendo la división $P(x)\div (x-(-1))$ $$\begin{array}{r|rrrrr}
& 1 & 2 & 2 & 2 & 1 \\
-1 & & -1 & -1 & -1 & 1\\
\hline & 1 & 1 & 1 & 1 & 0\end{array}$$ luego, por el momento, podemos escribir $$P(x)=(x+1)(x^3+x^2+x+1)$$ Si $P(x)$ tiene más raíces, éstas lo serán también del polinomio $x^3+x^2+x+1$. Como el término independiente es $1$, las posibles raíces enteras son, otra vez, $\{-1,1\}$. Para ensayarlas, utilizaremos el teorema del resto: si la división de $x^3+x^2+x+1$ entre $(x-(-1))$ tiene resto $0$, entonces $-1$ vuelve a participar como raíz de $P(x)$. Veámoslo: $$\begin{array}{r|rrrr}
& 1 & 1 & 1 & 1 \\
-1 & & -1 & 0 & -1 \\
\hline & 1 & 0 & 1 & 0 \end{array}$$ Como el resto es $0$, la raíz $r_1=-1$ aparece dos veces, luego su multiplicidad es $m_1=2$. Otra vez, por el teorema del factor, podemos escribir otro paso de factorización de $P(x)$ $$P(x)=(x-(-1))^2\,(x^2+1)$$ Observemos, ahora, que el polinomio que aparece como tercer factor, $x^2+1$, es primo, ya que no tiene raíces, pues si imponemos la condición de raíz, no encontramos ninguna: $x^2+1=0 \Leftrightarrow x=\sqrt{-1} \notin \mathbb{R}$
En resumen, el polinomio $P(x)$ sólo tiene una raíz, que es $-1$, y su multiplicidad es $2$; con lo cual puede escribirse ( teorema del factor ) de la forma $$P(x)=(x+1)^2\,(x^2+1)$$
$\square$
martes, 15 de noviembre de 2016
Cambio de base logarítmica
SOLUCIÓN
Podemos escribir la siguiente identidad numérica $$5=e^{\ln\,5} \quad \quad (1)$$
Sacando logaritmos en base $2$ en cada miembro de (1), $$\log_2\,5=\log_2\,(e^{\ln\,5})$$ y por las propiedades de los logaritmos, llegamos a $$\log_2\,5=\ln\,5 \cdot \log_2\,e \quad \quad (2)$$ Por otra parte, sea $$t\equiv\log_2\,e$$ entonces $$e=2^t$$ y sacando logaritmos naturales $$\ln\,e=t\,\ln\,2$$ con lo cual $$t=\dfrac{\ln\,e}{\ln\,2}\overset{\ln\,e=1}{=}\dfrac{1}{\ln\,2}$$ es decir $$\log_2\,e=\dfrac{1}{\ln\,2}$$ Sustituyendo esto en (2) $$\log_2\,5=\ln\,5 \cdot \dfrac{1}{\ln\,2} $$ esto es $$\log_2\,5= \dfrac{\ln\,5 }{\ln\,2} $$ y empleando ahora la calculadora $$\log_2\,5\overset{\text{4 c.d.}}{=} 2,3219 $$
$\square$
Cálculos con logaritmos
SOLUCIÓN.
$\log\,20=$
$=\log\,(2\cdot 10)$
$=\log\,2+\log\,10$
$=\log\,\dfrac{10}{5}+\log\,10$
$=\log\,10-\log\,5+\log\,10$
$=2\cdot \log\,10-\log\,5$
$\overset{\log\,10=1}{=}2\cdot 1-\log\,5$
$=2-\log\,5$
$\overset{\text{4 c.d.}}{=}2-0,6990$
$\overset{\text{4 c.d.}}{=}1,3010$
$\square$
Ecuaciones exponenciales
SOLUCIÓN.
$4=3^x$
$\ln\,4=\ln\,3^x$
$\ln\,4=x\,\ln\,3$
$x=\dfrac{\ln\,4}{\ln\,3}\overset{\text{4 c.d.}}{=} 1,2619$
$\square$
Resolver la ecuación
SOLUCIÓN.
Procedimiento I.
$(x+1)^8=2345$
$\left((x+1)^8\right)^{\frac{1}{8}}=(2345)^{\frac{1}{8}}$
$(x+1)^{8\cdot \frac{1}{8}}=(2345)^{\frac{1}{8}}$
$(x+1)^{1}=(2345)^{\frac{1}{8}}$
$x+1=(2345)^{\frac{1}{8}}$
$x=(2345)^{\frac{1}{8}}-1$
$x\overset{\text{4 c.d.}}{=}\pm 2,6384-1$
$x\overset{\text{4 c.d.}}{=}\left\{\begin{matrix}2,6384-1=1,6384 \\ -2,6384-1=-3,6384 \end{matrix}\right.$
Procedimiento II.
$(x+1)^8=2345$
$\ln\,(x+1)^8=\ln\,2345$
$8\cdot\ln\,(x+1)=\ln\,2345$
$\ln\,(x+1)=\dfrac{1}{8}\cdot\ln\,2345$
$\ln\,(x+1)=\ln\,2345^{\frac{1}{8}}$
$x+1=2345^{\frac{1}{8}}$
$x=(2345)^{\frac{1}{8}}-1$
$x\overset{\text{4 c.d.}}{=}\pm 2,6384-1$
$x\overset{\text{4 c.d.}}{=}\left\{\begin{matrix}2,6384-1=1,6384 \\ -2,6384-1=-3,6384 \end{matrix}\right.$
$\square$
martes, 25 de octubre de 2016
Contando el número de cifras significativas ...
a) $30\,000$
b) $0,00421$
c) $7,1\times 10^2$
d) $4\,000\,001$
e) $9,003\times 10^{-3}$
SOLUCIÓN.
Decimos que una cierta cifra de una determinada cantidad ( o número ) es significativa si ésta es relevante a la hora de expresar dicha cantidad. Pensemos pues en el orden de magnitud de cada cifra; ello nos dará la respuesta de si la cifra en cuestión es o no es significativa. Así, por ejemplo, consideremos el número $200$; al escribir su desarrollo de potencias de base $10$ -- recordemos que el sistema de numeración empleado es el decimal o de base $10$, que es posicional --, $200=2\times 10^2+ 0\times 10^1+0$, nos damos perfecta cuenta de que los dos ceros no son relevantes en dicha suma de términos pues corresponden a términos nulos del desarrollo ( no aportan valor a la cantidad ), luego sólo la cifra '$2$' ( la de las centenas ) es significativa. Diremos pues que $200$ tiene $1$ c.s.
a) a) Esta cantidad, $30\,000$, tiene $1$ c.s.: el '$3$' ya que, si sólo hay ceros a la derecha de la última cifra distinta de cero, por lo dicho arriba, éstos no se consideran en general cifras significativas; a menos que se fuerce la relevancia de los mismos, como por ejemplo, al decir que algo cuesta un euro y medio, pues al expresarlo numéricamente, deberemos escribir rigurosamente: $1,50$ euros, siendo en este caso el cero de las centésimas, también, cifra significativa, pues queremos significar con ello que operamos con una precisión del céntimo de euro ( no olvidemos que existen monedas de un céntimo ).
Otra forma de contar el número de cifras significativas consiste en expresar previamente la cantidad en notación científica ( recordemos lo que hemos dicho en el párrafo de introducción ), y, entonces, contar el número de cifras significativas de la mantisa es el número de cifras significativas de la cantidad dada, pues éste será el número de cifras significativas de la cantidad pedida. Así, $30\,000=3 \times 10^4$; y como la mantisa $3$ tiene una sola c.s., podemos decir que $30\,000$ tiene una sola c.s.
b) Esta cantidad, $0,00421$, tiene $3$ c.s.: la cifra de las unidades, la de las milésimas [el '$4$'], la de las diezmilésimas [el '$2$'], y la de las cienmilésimas [el '$1$']. Podemos contarlas también a partir de su expresión en notación científica, $4,21\times 10^{-3}$; como la mantisa tiene tres c.s., la cantidad pedida tiene este número de c.s.
c) $7,1\times 10^2$ tiene $2$ c.s., pues la mantisa tiene esas dos cifras significativas, el '$7$' y el '$1$'
d) En $4\,000\,001$, todas las cifras de este número son significativas, es decir, tiene $7$ c.s. Otra forma de contarlas pasa por -- como hemos hecho en otros apartados -- expresar dicha cantidad en notación científica, $4,000001\times 10^6$; como la mantisa tiene $7$ c.s., el número pedido tiene $7$ c.s.
$\square$
Presentación de los resultados de los cálculos con datos afectados de error
SOLUCIÓN. Como ya sabemos, el perímetro del rectángulo es igual a $2(a+b)$. Al realizar la operación, $2(\bar{a}+\bar{b})$, con todas las cifras significativas de los datos, obtenemos $15,842$ metros; ahora bien, no todas esas cifras del resultado son significativas. Como hay una operación de suma, ésta vendrá afectada por el error ( de medida ) de los dos datos ( las longitudes de los lados ) -- la multiplicación por $2$, no, pues el coeficiente no está afectado de error --, el número de cifras decimales significativas del resultado no puede ser mayor que el número de cifras decimales significativas del sumando que tenga menos precisión ( con menor número de cifras decimales significativas ), que es la medida de $a$, con $2$ cifras decimales significativas (c.d.s.), luego el resultado lo debemos a justar ( aproximar ) a $2$ cifras decimales significativas (c.d.s.). Diremos, pues, que el perímetro aproximado es de $15,84 \,\text{m}$
El área del rectángulo se obtiene haciendo $a\cdot b$. Al realizar la operación, $\bar{a}\cdot \bar{b}$, con todas las cifras significativas de los datos, obtenemos $12,29812$ metros cuadrados; ahora bien, no todas esas cifras del resultado son significativas. Como hay una operación de multiplicación, ésta viene afectada por el error de medida de las longitudes de los lados, así que, ahora ( multiplicación ) el número de cifras significativas del resultado no puede ser mayor que el número de cifras significativas del factor que tenga menos precisión ( con menor número de cifras significativas ), que es -- otra vez -- la medida de $a$, que tiene $3$ cifras significativas (c.s.), luego el resultado lo debemos a justar ( aproximar ) a $3$ cifras significativas (c.s.). Por consiguiente, el área aproximada es de $12,3 \,\text{m}^2$
$\square$
domingo, 23 de octubre de 2016
Ejercicios resueltos y comentados del examen realizado el miércoles 19/10/2016
Un problema en el que se aplican los logaritmos
SOLUCIÓN. Poniendo los datos en $C_f=C_i\cdot ( 1+i)^t$ llegamos a la ecuación $$50\,000=40\,000\,(1+0,04)^t$$ esto es $$\dfrac{5}{4}=1,04^t$$ que resolveremos sacando logaritmos ( da igual la base de los mismos ) en cada miembro $$\log\,\dfrac{5}{4}=\log\,1,04^t$$ que, por las propiedades de los logaritmos, queda $$\log\,\dfrac{5}{4}=t\cdot \log\,1,04$$ y despejando $t$ obtenemos $$t=\dfrac{\ln(5/4)}{\ln 1,04} \approx 5,7 \;\text{años} \overset{\text{por exceso}}{\approx} 5\; \text{años}\, \text{y}\;9\;\text{meses}$$
$\square$
Intervalos en la recta numérica
a) $\left| x+1\right|\le 3$
b) $\left| x-2\right|> 1$
c) estar en el entorno del punto ( de la recta real ) $5$ con radio $3$
SOLUCIÓN.
a)
$I=\{x \in \mathbb{R}:\left|x-(-1)\right|\le 3\}=\{x \in \mathbb{R}:\text{distancia}(x,-1) \le 3\}=$
$=[-1-3,-1+3] \subset \mathbb{R}$
$=[-4,2] \subset \mathbb{R}$
b)
$J=\{x \in \mathbb{R}:\left|x-2\right|\succ 1\}=\{x \in \mathbb{R}:\text{distancia}(x,2) \succ 1\}=$
$=(-\infty,2-1) \cup (2+1,+\infty)$
$=(-\infty,1) \cup (3,+\infty)$
c)
$K=E(5,3)=(5-3,5+3)\subset \mathbb{R}$
$=[2,8] \subset \mathbb{R}$
$\square$
Un ejercicio sobre aproximación y estudio del error
a) El error absoluto cometido en esta aproximación. ¿ Cuántas cifras significativas correctas hay en dicha aproximación ?
b) Si en lugar de considerar la aproximación anterior, aproximáramos por redondeo simétrico hasta las centésimas el número $\Phi$, ¿ qué número resultaría ? ¿ Cuál sería ahora el error absoluto ? ¿ Cuántas cifras significativas correctas habría en dicha aproximación ?
SOLUCIÓN.
a)
La cantidad exacta es, aquí, $x=\dfrac{1+\sqrt{5}}{2}$; y la aproximada, $\bar{x}=1,61$. Entonces, el error absoluto es
$$E\overset{\text{def}}{=}\left|x-\bar{x} \right|=\left|\dfrac{1+\sqrt{5}}{2}-1,61\right|\approx 0,008$$ Veamos si la cifra de las centésimas es correcta; para ello deberá cumplirse que el error absoluto sea menor que media unidad del orden de dicha cifra, esto es $$0,008 \overset{\text{?}}{<}\dfrac{1}{2}\cdot 10^{-2}=0,005$$ y es evidente que ésto no se cumple, luego la cifra de las centésimas ( el '1' ) no es correcta.
Veamos ahora si es correcta la cifra de las décimas ( el '6' ). Si lo es, debe cumplirse $$0,008 \overset{\text{?}}{<}\dfrac{1}{2}\cdot 10^{-1}=0,05$$ y es claro que sí se cumple, luego la cifra de las décimas es correcta. Por consiguiente, también es correcta la cifra de las unidades. Así que la aproximación $\bar{x}=1,61$ tiene dos cifras correctas ( la de las unidades y la de las décimas ), y una cifra dudosa, que corresponde a la de las centésimas.
b)
Si aproximamos por redondeo simétrico, $\bar{x}=1,62$, pues $x=\dfrac{1+\sqrt{5}}{2}=1,61803398\ldots$. El error absoluto es, ahora, $$E\overset{\text{def}}{=}\left|x-\bar{x} \right|=\left|\dfrac{1+\sqrt{5}}{2}-1,62\right|\approx 0,002$$ y, por tanto, $$0,002 {<} \dfrac{1}{2}\cdot 10^{-2}=0,005$$, luego la cifra de las centésimas ( el '2' ) es correcta, luego las cifra de las décimas y la de las unidades también son correctas. Así, pues, la aproximación por redondeo simétrico $\bar{x}=1,62$ tiene todas sus cifras correctas.
$\square$
Algunos ejercicios de cálculo
a) $\displaystyle \dfrac{\binom{3}{0}+\binom{3}{1}+\binom{3}{2}+\binom{3}{3}}{\binom{5}{4}}$
b) $\dfrac{2}{3}\div \left(\dfrac{2}{5}-1\right)^3$
c) $(1,\overset{\frown }{12}+2,\overset{\frown}{1})\cdot 0,5-0,5\overset{\frown}{2}$
d) $\displaystyle \binom{6}{4} \div 4!$
SOLUCIÓN.
a)
$\displaystyle \dfrac{\binom{3}{0}+\binom{3}{1}+\binom{3}{2}+\binom{3}{3}}{\binom{5}{4}} = \dfrac{\frac{3!}{0!(3-0)!}+\frac{3!}{1!(3-1)!}+\frac{3!}{2!(3-2)!}+\frac{3!}{3!(3-3)!}}{\frac{5!}{4!(5-4)!}}=\dfrac{1+3+3+1}{5}=\dfrac{8}{5}$
Nota: También podemos escribir directamente el valor del numerador, que es $2^3=8$. Esto es así por una de las propiedades de los números combinatorios que hemos visto en clase, que es la siguiente: $$\binom{n}{0}+\binom{n}{1}+\ldots+\binom{n}{n-1}+\binom{n}{n}=2^n$$
b)
$\dfrac{2}{3}\div \left(\dfrac{2}{5}-1\right)^3=$
$=\dfrac{2}{3}\div \left(-\dfrac{3}{5}\right)^3$
$=\dfrac{2}{3}\div \left( -\left(\dfrac{3}{5}\right)^3\right)$
$=-\dfrac{2}{3}\div \left(\dfrac{3}{5}\right)^3$
$=-\dfrac{2}{3}\div \dfrac{3^3}{5^3}$
$=-\dfrac{2}{3}\cdot \text{inverso}\left( \dfrac{3^3}{5^3}\right)$
$=-\dfrac{2}{3}\cdot \dfrac{5^3}{3^3}$
$=-\dfrac{2\cdot 5^3}{3\cdot 3^3}$
$=-\dfrac{250}{81}$
c)
$(1,\overset{\frown }{12}+2,\overset{\frown}{1})\cdot 0,5-0,5\overset{\frown}{2}=$
$= (\dfrac{112-1}{99}+\dfrac{21-2}{9})\cdot \dfrac{1}{2}-\dfrac{52-5}{90}$
$= (\dfrac{37}{33}+\dfrac{19}{9})\cdot \dfrac{1}{2}-\dfrac{47}{90}$
$= \dfrac{320}{99}\cdot \dfrac{1}{2}-\dfrac{47}{90}$
$= \dfrac{160}{99}-\dfrac{47}{90}$
$= \dfrac{361}{330}$
d)
$\displaystyle \binom{6}{4} \div 4!=$
$=\displaystyle \dfrac{\binom{6}{4}}{4!}$
$=\displaystyle \dfrac{\frac{6!}{4!\cdot (6-4)!}}{4!}$
$=\displaystyle \dfrac{15}{24}$
$=\displaystyle \dfrac{5}{8}$
$\square$
Ejercicios diversos de cálculo con: radicales, y notación científica
a) La masa de la Tierra es $5,9722 \times 10^{24} \,\text{kg}$ y la de la Luna, $7,349 \times 10^{22}\,\text{kg}$. ¿ Cuántas veces es mayor la masa de la Tierra que la de la Luna ?.
b) El radio de la Tierra es $6371\,\text{km}$ y el de la Luna, $1737 \, \text{km}$. ¿ Cuántas veces es mayor el volumen de la Tierra que el de la Luna ?
c) Determínese una expresión equivalente a $\dfrac{1}{\sqrt{2}-\sqrt{3}}$ que no tenga radicales en el denominador
d) Determínese una expresión equivalente a $\dfrac{4}{\sqrt[5]{2^3}}$ que no tenga radicales en el denominador
e) Constrúyase el triángulo de Tartaglia hasta la séptima fila
SOLUCIÓN.
a) El número de veces que la masa de la Tierra es mayor que la de la Luna es igual a $$\dfrac{5,9722 \times 10^{24}}{7,349 \times 10^{22}} \approx 81$$
b) El número de veces que el volumen de la Tierra es mayor que el de la Luna es igual al cociente de los respectivos volúmenes, $$\dfrac{\frac{4}{3}\,\pi\,(6371)^3}{\frac{4}{3}\,\pi\,(1737)^3}=\left( \dfrac{6371}{1737} \right)^3 \approx 49$$
c)
$\dfrac{1}{\sqrt{2}-\sqrt{3}}=\dfrac{1}{\sqrt{2}-\sqrt{3}}\cdot \dfrac{\sqrt{2}+\sqrt{3}}{\sqrt{2}+\sqrt{3}}=\dfrac{\sqrt{2}+\sqrt{3}}{(\sqrt{2}-\sqrt{3})(\sqrt{2}+\sqrt{3})}=\dfrac{\sqrt{2}+\sqrt{3}}{(\sqrt{2})^2-(\sqrt{3})^2}=$
$=\dfrac{\sqrt{2}+\sqrt{3}}{2-3}=\dfrac{\sqrt{2}+\sqrt{3}}{-1}=-(\sqrt{2}+\sqrt{3})$
d) $\dfrac{4}{\sqrt[5]{2^3}}=\dfrac{4}{\sqrt[5]{2^3}}\cdot \dfrac{\sqrt[5]{2^{5-3}}}{\sqrt[5]{2^{5-3}}}=\dfrac{4\,\sqrt[5]{2^{2}}}{\sqrt[5]{2^{3}}\cdot \sqrt[5]{2^{2}}}=\dfrac{4\,\sqrt[5]{2^{2}}}{\sqrt[5]{2^{2}\cdot 2^3}}=\dfrac{4\,\sqrt[5]{2^{2}}}{\sqrt[5]{2^5}}=\dfrac{4\,\sqrt[5]{4}}{2}=2\,\sqrt[5]{4}$
$\square$
jueves, 6 de octubre de 2016
Suma i producte dels $n$ primers termes d'una successió geomètrica
Enunciat:
El segon terme d'una successió geomètrica és igual a $4$ i el sisè terme és igual a $3$
Us demanem:
a) El valor de la suma dels vint primers termes d'aquesta successió: $a_1+a_2+\ldots+a_{20}$.
b) El valor del producte dels deu primers termes d'aquesta successió: $a_1 \cdot a_2 \cdot a_3 \cdot \ldots \cdot a_{20}$
Resolució:
a)
Entre el segon i el sisè terme hi ha tres termes; per tant, el sisè terme $a_6$ representa el cinquè terme de la seqüència $\{a_2, a_3, \ldots, a_6 \}$. Llavors
$a_6=a_2 \cdot r^4$
(on $r$ representa la raó de la successió geomètrica)
Tenint en compte els valors donats a l'enunciat
$3=4 \cdot r^4$
d'on obtenim
$r=\bigg(\dfrac{3}{4}\bigg)^{\frac{1}{4}}$
Per calcular la suma dels $n$ primers termes consecutius d'una successió aritmètica de diferència igual a $d$ podem fer ús del resultat
$s_n=a_1 \cdot \dfrac{r^{n}-1}{r-1} \quad \quad (1)$
Veiem, doncs, que cal calcular els valors del primer terme:
El valor del primer és igual a
$a_1=a_2 \cdot \dfrac{1}{r}$
que, tenint en compte els valors de l'enunciat, dóna
$a_1 = \ldots = 4 \cdot 2^{\frac{1}{2}} \cdot 3^{-\frac{1}{4}} \quad \quad (2)$
Llavors, fent el càlcul indicat (1), el valor de la suma demanada és igual a
$s_{20} \approx 47,2407$
b)
Sabem que el producte $p_n$ dels $n$ primers termes d'una successió geomètrica és igual a
$p_n=\bigg(a_1 \cdot a_n \bigg)^{\frac{n}{2}} \quad \quad (3)$
Ens falta calcular el valor del vintè terme per poder emprar aquest resultat. Calculem-lo a partir de
l'expressió del terme general d'una successió geomètrica i del valor de $a_1$ (2)
$a_n=a_1 \cdot r^{n-1} \quad (n=1,2,3,\ldots)$
$a_{20}=a_1 \cdot r^{19} = \ldots = \dfrac{81 \, \sqrt{3}}{128}$
Llavors, de l'expressió (3) i del valor del primer terme (2), trobem
$p_n = \big(a_1 \cdot a_n \big)^{10} \approx 5386461$
$\square$
miércoles, 28 de septiembre de 2016
Demostrar que $\sqrt{2}$ no es un número racional
SOLUCIÓN. Vamos a utilizar el método de demostración por contradicción. Supongamos lo contrario de lo queremos demostrar: $\sqrt{2}$ sí es un número racional. Entonces existen $m,n \in \mathbb{N}$ tales que $\sqrt{2}=\dfrac{m}{n}$ siendo $\text{mcd}(m,n)=1$ ( la fracción es irreducible ). De ahí se deduce que, elevando al cuadrado los dos miembros, $2\,n^2=m^2 \quad \quad (1)$, lo cual significa que $m^2$ es múltiplo de $2$, así que $m$ también debe ser un múltiplo de $2$, por lo tanto existe $p \in \mathbb{N}$ tal que $m=2\,p \quad \quad (2)$.
Sustituyendo $m$ de (2) en (1) llegamos a $$2\,n^2=(2p)^2$$ esto es $$2\,n^2=4p^2$$ y por tanto $$n^2=2\,p^2$$ pero ésto quiere decir que $n^2$ es múltiplo de $2$ y, por consiguiente, también $n$ ha de ser múltiplo de $2$. Llegados a este punto, recopilemos lo que hemos encontrado: $n$ y $m$ son múltiplos de $2$, de lo cual deducimos que $\text{mcd}(n,m)\neq 1$. Pero ésto contradice la suposición inicial, así que debemos negarla, quedando de esta forma demostrada la afirmación del enunciado. $\square$
sábado, 17 de septiembre de 2016
Recuentos combinatorios empleando el método constructivo
a) que sean pares y menores que $5000$
b) que sean pares y menores que $3000$
c) que sean pares, menores que $5000$ y mayores o iguales que $3000$
SOLUCIÓN. Emplearemos el método constructivo en todos y cada uno de los apartados.
a)
Podemos elegir la cifra de la unidades de millar entre el conjunto $\{0,2,3\}$, teniendo por tanto $3$ posibilidades de elección para esta cifra. La cifra de las centenas y la de las decenas podemos elegirlas entre todas las cifras del conjunto $\{0,2,3,5,7\}$, luego hay $5$ posibilidades de elección para cada una; finalmente, la cifra de las unidades sólo puede elegirse entre $\{0,2\}$ pues los números a construir han de ser pares. Así pues, por el principio multiplicativo del recuento, hay un total de $3 \cdot 5 \cdot 5 \cdot 2=150$ números que reúnen las condiciones pedidas en el primer apartado.
b)
Debemos ahora elegir la cifra de la unidades de millar entre el conjunto $\{0,2\}$, teniendo por tanto $2$ posibilidades de elección para esta cifra. La cifra de las centenas y la de las decenas podemos elegirlas entre todas las cifras del conjunto $\{0,2,3,5,7\}$ ( igual que en el primer apartado ), luego hay $5$ posibilidades de elección para cada una; finalmente, y también como en el primer apartado, la cifra de las unidades sólo puede elegirse entre $\{0,2\}$ pues los números a construir han de ser pares. Así pues, por el principio multiplicativo del recuento, hay un total de $2 \cdot 5 \cdot 5 \cdot 2=100$ números que reúnen las condiciones pedidas en el segundo apartado.
c)
Restando los resultados de los dos apartados anteriores, vemos que hay $150-100=50$ números que cumplen la condición del tercer apartado.
$\square$
miércoles, 14 de septiembre de 2016
Sentando personas en una fila de butacas
SOLUCIÓN.
Vamos a resolver el problema siguiendo un procedimiento constructivo y aplicando el principio multiplicativo del recuento. Para ello, y siguiendo un orden, debemos pensar ( simular ) de cuántas maneras podemos ocupar cada una de las butacas de la fila, teniendo en cuenta la condición del enunciado ( no puede haber dos chicos ni dos chicas sentados en butacas consecutivas ). El orden que seguiremos en la asignación de butaca para ir llenando la fila será de izquierda a derecha ( llegaríamos al mismo resultado si cambiásemos el orden yendo de derecha a izquierda ).
Consideremos la primera butaca de la fila; en ella pueden sentarse cualquiera de las seis personas, ya se trate de un chico o bien de una chica, por lo que tenemos $\mathbb{6}$ posibilidades de elección para este primer asiento. La segunda butaca sólo puede ser ocupada por tres de las personas de género opuesto al de la persona que ha ocupado la primera butaca, luego hay $\mathbb{3}$ posibilidades de elección para este segundo asiento. La tercera butaca tendrá que ser ocupada por una persona del mismo género que el de la persona que ocupa la primera, luego sólo hay $2$ elecciones posibles para ese asiento ( ya que una de las tres, sea chico o bien sea chica, ya está sentada ). Para la cuarta butaca, tendremos otras $\mathbb{2}$ elecciones posibles, pues ya se ha sentado una persona de género opuesto al de la persona sentada en la segunda butaca. Así, para la quinta y para la sexta butacas, sólo hay $\mathbb{1}$ elección posible para cada una de ellas, que corresponde a la única persona de cada género, que quedan aún por sentarse.
Entonces, por el principio de multiplicación, el grupo se puede sentar de $6 \cdot 3 \cdot 2 \cdot 2 \cdot 1 \cdot 1 = 72$ maneras posibles, respetando la condición dada en el enunciado. $\square$
miércoles, 7 de septiembre de 2016
Ejercicios resueltos y comentados del examen extraordinario de Septiembre, realizado el Jueves 1/09/2016
Un ejercicio de geometría analítica ( recta que pasa por dos puntos dados del plano )
a) Determinar la ecuación de la recta en forma explícita
b) Hallar el valor de la pendiente de dicha recta y el del ángulo que forma ésta con el eje de abscisas ( graduando los dos ejes de la misma forma )
c) Calcular el valor de la ordenada del punto de corte de la recta con el eje de ordenadas
SOLUCIÓN.
a) La abscisa es la misma en ambos puntos, luego la recta $r$ pedida es perpendicular al eje de abscisas y su ecuación es $r:x=1$
b) Al tratarse de una recta perpendicular al eje de abscisas, el ángulo que forma con el eje de abscisas es de $90^{\circ}$, luego la pendiente es infinita
c) La recta es paralela ( y no coincidente ) al eje de ordenadas, luego no lo corta.
$\square$
Resolver los siguientes problemas de geometría ...
a) Calcular el volumen y el área lateral de un cono de base circular de $4$ decímetros de generatriz y de $3$ decímetros de radio de la base
b) Calcular el área del triángulo equilátero inscrito en una circunferencia de $3$ decímetros de radio
SOLUCIÓN.
a)
El volumen del cono es igual a una tercera parte del producto del área de la base ( que es un círculo de radio $3$ dm ) por la altura ( que denotamos por $h$ ), esto es $$V=\dfrac{1}{3}\cdot \pi\cdot 3^2\cdot h \quad \quad (1)$$ Es claro que tenemos que calcular $h$. Observando la figura vemos que, dado un punto cualquiera de la circunferencia de la base, la altura, la generatriz y el radio conforman un triángulo rectángulo. Aplicando el teorema de Pitágoras, podemos escribir $4^2=3^2+h^2$, luego $h=\sqrt{4^3-3^2}=\sqrt{7}\,\text{dm}$. Así, de (1), obtenemos $V=\dfrac{1}{3}\cdot \pi\,3^2\cdot \sqrt{7}=3\,\pi\,\sqrt{7}\,\text{dm}^3$
El área lateral del cono viene dada por la fórmula $A_\ell=\pi\,r\,g$ ( justificada en clase ). Con los datos, obtenemos $A_\ell=\pi\cdot 3 \cdot 4 = 12 \,\pi\, \text{dm}^2$
b)
El área del triángulo inscrito en la circunferencia ( ver la figura de abajo ) es igual a un medio de la longitud del lado de la base por la altura correspondiente, esto es, $A=\dfrac{1}{2}\cdot 2y \cdot (3+x)=y\cdot(3+x) \quad \quad (2)$.
Utilizaremos el triángulo rectángulo que se aprecia en la figura para calcular $x$ e $y$.
Para ello emplearemos las razones trigonométricas seno y coseno ( NOTA: Podríamos incluso prescindir de la trigonometría elemental para calcular estas magnitudes ). Así, $y=3\cdot \cos\,30^{\circ}=\dfrac{3\,\sqrt{3}}{2}\, \text{dm}$ y $x=3\cdot \sin\,30^{\circ}=\dfrac{3}{2}\, \text{dm}$. Entonces, poniendo estos resultados en (2) obtenemos, $$A=\dfrac{3\,\sqrt{3}}{2} \cdot ( 3+\dfrac{3}{2} )=\dfrac{27\,\sqrt{3}}{4}\,\text{dm}^2$$
$\square$
Cálculo de probabilidades en extracciones sucesivas de bolas de una urna
a) con reemplazamiento ( a la urna ) de las bolas que se van sacando
b) sin reemplazar las bolas que se van sacando
SOLUCIÓN
Denotemos por $B_i$ al suceso extraer bola blanca en la i-ésima extracciónn ( $i=1,2,3$ ) y por $N_i$ al suceso extraer bola negra en la i-ésima extracciónn ( $i=1,2,3$ ). Entonces, el sucesos extraer tres bolas del mismo color ( que denotamos por $C$ ) viene dado por $(B_1 \cap B_2 \cap B_3 ) \cup ( N_1 \cap N_2 \cap N_3 )$. Es claro que los sucesos $B_1 \cap B_2 \cap B_3$ y $N_1 \cap N_2 \cap N_3$ son disjuntos ( incompatibles ), luego $$P((B_1 \cap B_2 \cap B_3 ) \cup (N_1 \cap N_2 \cap N_3))=P(B_1 \cap B_2 \cap B_3 )+P(N_1 \cap N_2 \cap N_3)$$
a)
En las condiciones del primer apartado, $$P(B_1 \cap B_2 \cap B_3 )\overset{\text{s. independientes}}{=}P(B_1)\cdot P(B_2) \cdot P(B_3)=\dfrac{3}{8}\cdot \dfrac{3}{8} \cdot \dfrac{3}{8}=\dfrac{27}{512}$$ y $$P(N_1 \cap N_2 \cap N_3 )\overset{\text{s. independientes}}{=}P(N_1)\cdot P(N_2)\cdot P(N_3)=\dfrac{5}{8}\cdot \dfrac{5}{8} \cdot \dfrac{5}{8}=\dfrac{125}{512}$$ por tanto $$P(C)=\dfrac{27}{512}+\dfrac{125}{512}=\dfrac{19}{64}\approx 29,7\,\%$$
NOTA 1: Si bien no es indispensable, puede ayudar la realización de un diagrama de árbol
OBSERVACIÓN 1. Otra forma de resolverlo consiste en emplear las fórmulas combinatorias y, directamente, el principio de Laplace. Esto se justifica considerando que cada bola -- sea blanca o negra -- tiene las mismas posibilidades de ser elegida, con lo cual, el espacio muestral está formado por sucesos equiprobables. Entonces $P(C) \overset{\text{Laplace}}{=} \dfrac{N(C)}{N}$. En el caso que nos ocupa, $N(C)=VR_{3,3}+VR_{5,3}=5^3+3^3=152$ y $N=VR_{5+3,3}=8^3=512$, por tanto $P(C)=\dfrac{152}{512}=\dfrac{19}{64} \approx 29,7\,\%$
b)
En las condiciones del segundo apartado, $$P(B_1 \cap B_2 \cap B_3 )\overset{\text{p. condicionada}}{=}P(B_1)\cdot P(B_2|B_1)\cdot P(B_3|B_1 \cap B_2)=\dfrac{3}{8}\cdot \dfrac{2}{7} \cdot \dfrac{1}{6}=\dfrac{1}{56}$$ y $$P(N_1 \cap N_2 \cap N_3 )\overset{\text{p. condicionada}}{=}P(N_1)\cdot P(N_2|N_1)\cdot P(N_3|N_1 \cap N_2)=\dfrac{5}{8}\cdot \dfrac{4}{7} \cdot \dfrac{3}{6}=\dfrac{5}{28}$$ por tanto $$P(C)=\dfrac{1}{56}+\dfrac{5}{28}=\dfrac{11}{56}\approx 19,6\,\%$$
NOTA 2: Si bien no es indispensable, puede ayudar la realización de un diagrama de árbol
OBSERVACIÓN 2. Como hemos comentado en el primer apartado, otra forma de resolverlo pasa por empleando las fórmulas de combinatoria para aplicar el principio de Laplace: $P(C) \overset{\text{Laplace}}{=} \dfrac{N(C)}{N}$. En el caso que nos ocupa ahora, $N(C)=\binom{3}{3}+\binom{5}{3}$ y $N=\binom{5}{5+3}$, por tanto $P(C)=\dfrac{\binom{3}{3}+\binom{5}{3}}{\binom{5}{5+3}}=\dfrac{11}{56} \approx \binom{3}{3}+\binom{5}{3}$
$\square$
Ejercicios de combinatoria
a) Formar una comisión de $4$ personas, elegidas entre un grupo que consta de $6$ personas
b) Elaborar banderas de señales de $3$ franjas verticales con telas de $2$ colores
c) Escribir "palabras" con las letras de la palabra MISSISSIPI, de manera que en cada palabra aparezca cada una de las letras y con el mismo número de repeticiones de cada una que se dan en la palabra de referencia
d) Distribuir $5$ caramelos de sabores distintos entre $3$ personas
SOLUCIÓN.
a) No importa el orden de colocación de las personas elegidas para formar parte de la comisión y, obviamente, no podemos repetir personas en la elección, luego el problema es de combinaciones ordinarias. Así, tenemos $C_{6,4}=\binom{6}{4}=15$ maneras distintas de formar la comisión
b) Es posible repetir color a la hora de coser las franjas para elaborar una bandera y, por supuesto, es relevante el orden ( de izquierda a derecha ) en la disposición del color, luego el problema es de variaciones con repetición: $VR_{2,3}=2^3=8$. En otras palabras, podemos elegir dos colores para cada una de las tres franjas, luego por el principio de elecciones independientes tenemos $2 \cdot 2 \cdot 2= 8 $ banderas posibles.
c) La palabra de referencia ( MISSISSIPI ) consta de diez letras, entre las cuales hay algunas que aparecen repetidas. Además, es evidente que importa el orden de colocación de las letras a la hora de permutarlas para formar nuevas palabras, por tanto el tipo de problema es de permutaciones con elementos repetidos, por lo que el número pedido es $PR_{10}^{1,4,4,1}=\dfrac{10!}{1!\cdot 4! \cdot 4! \cdot 1!}=6300$ palabras
d)
Es evidente que puede haber distribuciones en las que alguna persona se quede sin caramelo/s, luego debemos pensar la situación asignando personas a cada uno de los tres caramelos. Para el primer caramelo tenemos tres posibilidades a la hora de asignarle propietario, y lo mismo para los otros cuatro caramelos. Entonces, por el principio multiplicativo, el número de maneras de distribuir el conjunto de caramelos es igual a $3\cdot 3 \cdot 3 \cdot 3 \cdot 3 $, es decir $VR_{3,5}=3^5=243$.
$\square$
Ejercicio de estadística descriptiva de una variables, con sus valores agrupados en clases
Elaborar el diagrama de tallo y hojas. A continuación, agrupar los valores en intervalos, todos ellos de amplitud igual a $10$, y determinar los siguientes parámetros estadísticos: moda, cuartiles, media,varianza, disviación estándar, coeficiente de variación, rango, y rango intercuartílico. Elaborar, también, los histogramas y el diagrama de caja y bigotes.
SOLUCIÓN.
Diagrama de tallo y hojas:
Si observamos el diagrama de tallo y hojas, y realizamos un estudio discreto del conjunto de datos, vemos que la distribución es bimodal, pues dos de los valores ( y no sólo uno ) se repiten con mayor frecuencia; éstos son $25$ y $35$. Ahora bien, es mucho más razonable que hagamos un estudio continuo de la distribución, agrupando los datos ( tal como se pide en el enunciado ).
A continuación mostramos la tabla de frecuencias ( y frecuencias acumuladas ) que resulta de la agrupación de los datos en los intervalos que figuran en la primera columna ( las marcas de clase son los números de la segunda columna ):
Así, vemos que la moda está en el intervalo $[30,40)$; precisando un poco más y empleando la semejanza de triángulos al trazar los segmentos que une el punto superior derecha (respectivamente, superior izquierda) del rectángulo de mayor altura con el punto inferior izquierda ( respectivamente, inferior derecha ).
La abscisa del punto de intersección de estos segmentos nos da el valor de la moda. Veamos qué resulta de los cálculos:
$$\dfrac{a}{15-9}=\dfrac{10-a}{15-12}$$ luego $$a=\dfrac{20}{3}$$ y, por tanto, la moda es igual aproximadamente ( la agrupación en clases no da resultados exactos ) a $$M_o \approx 30+a = 36,7$$
Diagrama de caja y bigotes:
A partir del estudio continuo ( datos agrupados en intervalos/classes ) y trabajando con el histograma de frecuencias acumuladas ( cuarta columna de la tabla ), obtenemos el siguiente resultado aproximado ( recordemos que al agrupar en intervalos, renunciamos a los resultados exactos ).
Se omiten los cálculos rutinarios de proporcionalidad con los triángulos semejantes ( similares al que se ha detallado arriba, para el cálculo de la moda ) que se forman al trabajar con la línea poligonal de frecuencias acumuladas, en el correspondiente histograma:
Nota: En la lista no hay datos atípicos, pues ninguno de ellos cumple alguna de estas condiciones: $$ x < Q_1-RIC$$ $$ x > Q_3+RIC$$
Se ve con claridad que el rango es igual a $56-10=46|$
El cálculo de los demás parámetros puede realizarse con ayuda de la calculadora científica, para ello debemos introducir las cuatro parejas (marca de clase, frecuencia respectiva) que tenemos anotadas ya en la tabla de frecuencias, y consultar los resultados en la calculadora.
Introducción de datos ( en una calculadora científica básica Casio fx-82MS ):
MODE 2 (modo estadístico con 1 variable )
15;6 M+
25;9 M+
35;15 M+
45;12 M+
Consultando los valores de los parámetros:
Tecleando S-VAR ( con los datos introducidos ). Se puede comprobar que aparecen los siguientes resultados [Nota: Conviene, sin embargo, escribir las definiciones de dichos parámetros ]
media: $\bar{x}\overset{\text{def}}{=}\dfrac{1}{N}\,\displaystyle \sum_{i=1}^{4} x_i\,f_i\approx 32,9$
varianza: $s_{x}^2\overset{\text{def}}{=}\dfrac{1}{N}\,\displaystyle \sum_{i=1}^{4} x_{i}^{2}\,f_i-(\bar{x})^2\approx 102,6$
desviación estándar: $s_x\overset{\text{def}}{=}\sqrt{s_{x}^2}\approx 10,1$
coeficiente de variación: $CV\overset{\text{def}}{=}\dfrac{s_x}{\bar{x}} \approx 31\,\%$
$\square$
martes, 30 de agosto de 2016
¿ Cuál es el ángulo que forman las manecillas del reloj ... ?
SOLUCIÓN. Tomemos la semirrecta que pasa por el centro del círculo horario y el punto que marca las 12:00, como referencia del cero de medida angular; y, establecemos el sentido positivo de giro, el correspondiente al movimiento de las manecillas.
Llamemos $\varphi_{h}$ al ángulo que forma la manecilla de las horas con la semirrecta de referencia, y $\varphi_{m}$ al ángulo que forma la manecilla de los minutos con la semirrecta de referencia. Entonces, es fácil ver ( se recomienda hacer una figura de la hora indicada ) que el ángulo pedido ( que llamaremos $\theta$ ) viene dado por la diferencia de ambos ángulos $$\theta=\left|\varphi_{h}-\varphi_{m}\right|$$
Calculemos ahora dichos ángulos. Para ello, debemos tener en cuenta que el movimiento ( circular ) de las manecillas es uniforme, cada una con su respectiva velocidad angular. Así, podemos plantear las siguientes proporciones ( entre el ángulo con respecto a la semirrecta de referencia ) y el tiempo correspondiente ) para calcular uno y otro ángulo: $$\dfrac{\varphi_{h}}{360^{\circ}}=\dfrac{(15-12)\cdot 60+40}{(24-12)\cdot 60} \Rightarrow \varphi_{h}=110^{\circ}$$
$$\dfrac{\varphi_{m}}{360^{\circ}}=\dfrac{40}{60} \Rightarrow \varphi_{m}=240^{\circ}$$
Finalmente, obtenemos el ángulo pedido $$\theta=\left|110^{\circ}-240^{\circ}\right|=130^{\circ}$$
$\square$
martes, 14 de junio de 2016
Ejercicios resueltos del examen global de Junio ( temas 1-16 ), realizado el Lunes 13/06/2016
Recta que pasa por dos puntos del plano
a) La ecuación de la recta
b) Calcular la ordenada de un punto de la recta cuya abscisa es $2$
c) Calcular la abscisa de un punto de la recta cuya ordenada es $6$
SOLUCIÓN.
a)
La ecuación de la recta en forma explícita viene dada por $y=m\,x+k$. Para determinar los coeficientes $m$ y $k$, procedemos de la siguiente manera:
Si el punto $A$ está sobre la recta, se cumple: $2=-1\cdot m+k$
Si el punto $B$ está sobre la recta, se cumple: $5=3\cdot m+k$
Resolviendo el sistema de ecuaciones obtendremos los valores de $m$ y $k$. Despejando $k$ de sendas ecuaciones e igualando los segundos miembros $$2+m=5-3m$$ agrupando y despejando $m$ resulta $m=\dfrac{3}{4}$; y, sustituyendo este resultado en cualquiera de las dos ecuaciones, encontramos el valor del otro coeficiente: $k=\dfrac{11}{4}$. Así, la ecuación de la recta es $$r:y=\dfrac{3}{4}\,x+\dfrac{11}{4}$$
b)
La ordenada de un punto cuya abscisa es $2$ es la imagen de $2$ por la función $f(x)= \dfrac{3}{4}\,x+\dfrac{11}{4}$, esto es, $f(2)=\dfrac{3}{4}\cdot 2+\dfrac{11}{4}=\dfrac{17}{4}$
c)
Si $y=6$, entonces se tiene que $6=\dfrac{3}{4}\,x+\dfrac{11}{4}$; despejando $x$ obtendremos el valor de la abscisa de un punto que está sobre la recta y cuya ordenada es $6$, llegando a $x=\dfrac{13}{3}$
$\square$
Factorización de polinomios
SOLUCIÓN. El conjunto de raíces viene dado por $\{x \in \mathbb{R}: P(x)=0\}$, por lo que imponiendo la condición nos encontramos con una ecuación bicuadrada $$x^4-29\,x^2+100=0$$ que resolveremos donatando $x^2$ por $y$; así, $x^4=(x^2)^2=y^2$, con lo cual la ecuación original se transforma en $y^2-29\,y+100=0$ que es una ecuación cuadrática y, por tanto, sabemos resolverla: $$y^2-29\,y+100=0 \Leftrightarrow y=\dfrac{-(-29)\pm \sqrt{(-29)^2-4 \cdot 1 \cdot 100}}{2 \cdot 1}=\left\{\begin{matrix}4 \\ \\ 25\end{matrix}\right.$$ Deshaciendo ahora el cambio que hemos efectuado al principio $$x=\sqrt{y}$$ luego, si $y=4$ obtenemos $x=\sqrt{4}=\pm 2$; y, si $y=25$ obtenemos $x=\sqrt{25}=\pm 5$. El conjunto de raíces del polinomio es pues $$\{-5,-2,2,5\}$$
$\square$
Trigonometría elemental
SOLUCIÓN. Podemos descomponer el octágono regular inscrito en la circunferencia en ocho triángulos isósceles que tienen por vértice común el centro de la circunferencia circunscrita ( que llamaremos $O$ ), y cuyo ángulo ( central ) es igual a $\dfrac{360^{\circ}}{8}=45^{\circ}$. Entonces el área del octágono ( que denotamos por $\mathcal{A}_{o}$ ) es igual a ocho veces el área de uno de esos triángulos , que denotaremos por $\mathcal{A}_{t}$.
Vamos a calcular, pues, el área $\mathcal{A}_{t}$. Denotemos por $\ell$ el lado del octágono ( que corresponde al lado desigual de dicho tríangulo ) y por $a$ a la altura correspondiente a dicho lado. Entonces, $\mathcal{A}_{t}=\dfrac{1}{2}\,\ell \cdot a$. Necesitamos, por tanto, calcular $\ell$ y $a$.
La recta que contiene $a$ divide al triángulo en dos triángulos rectángulos. La hipotenusa de dicho triángulo es igual al radio de la circuferencia circunscrita, y por tanto igual a $1$ decímetro. El valor del ángulo de vértice $O$ de dicho triángulo recángulo es igual ( por lo que acabamos de decir ) a $\dfrac{45^{\circ}}{2}$. Aplicando las razones trigonométrica seno y coseno de dicho ángulo, encontramos:
$$a=1 \cdot \cos \,\dfrac{45^{\circ}}{2}$$ y $$\ell/2=1 \cdot \sin \,\dfrac{45^{\circ}}{2} \; \text{y por tanto}\; \ell = 2 \cdot \sin \,\dfrac{45^{\circ}}{2}$$
luego $$\mathcal{A}_{t}=\dfrac{1}{2}\,( 1 \cdot \cos \,(\dfrac{45^{\circ}}{2})) \cdot ( 2 \cdot \sin \,(\dfrac{45^{\circ}}{2}))$$ y simplificando $$\mathcal{A}_{t}=\cos \,(\dfrac{45^{\circ}}{2}) \cdot \sin \,(\dfrac{45^{\circ}}{2})$$
Así, el área del octágono es igual a $$\mathcal{A}_{o}= 8 \cdot \cos \,(\dfrac{45^{\circ}}{2}) \cdot \sin \,(\dfrac{45^{\circ}}{2}) \approx 2{,}8 \; \text{dm}^2$$
$\square$
Extracciones sucesivas de bolas de una urna ...
a) con reemplazamiento de las bolas que se van sacando
b) sin reemplazamiento
SOLUCIÓN.
Nota. Para resolver este problema puede ayudar el dibujar un diagrama de árbol, si bien no es necesario. Recomiendo al lector que lo haga. También podemos llegar a la solución empleando el cálculo combinatorio ( tal como hemos hecho en otras ocasiones ), sin embargo, ahora, vamos a emplear el lenguaje de sucesos y la noción de probabilidad condicionada.
Denotando:
$B_1$: obtener bola blanca en la primera extracción
$N_1$: obtener bola negra en la primera extracción
$B_2$: obtener bola blanca en la segunda extracción
$N_2$: obtener bola negra en la segunda extracción
$B_3$: obtener bola blanca en la tercera extracción
$N_3$: obtener bola negra en la tercera extracción
a)
En este caso, al reemplazar las bolas que se van extrayendo no alteramos el contenido de la urna y, por tanto, el resultado de una extracción es independiente del resultado de las extracciones anteriores. Empleando el álgebra de sucesos, podemos escribir la probabilidad pedida como:
$P((B_3 \cap B_2 \cap B_1) \cup (N_3 \cap N_2 \cap N_1))=$
$=P(B_3 \cap (B_2 \cap B_1) ) + P(N_3 \cap (N_2 \cap N_1))=$
$=P(B_3 | B_2 \cap B_1)\cot P(B_2 \cap B_1) + P(N_3 | N_2 \cap N_1)\cdot P(N_2 \cap N_1)$
$=P(B_3 | B_2 \cap B_1)\cdot P(B_2 | B_1)\,P(B_1) + P(N_3 | N_2 \cap N_1)\cdot P(N_2 | N_1)\cdot P(N_1)$
$=P(B_3 | B_2 \cap B_1)\cdot P(B_2 \cap B_1) + P(N_3 | N_2 \cap N_1)\cdot P(N_2 \cap N_1)$
$=P(B_3 | B_2 \cap B_1)\cdot P(B_2|B_1)\cdot P(B_1) + P(N_3 | N_2 \cap N_1)\cdot P(N_2|N_1)\cdot P(N_1)$
$=\dfrac{4}{7} \cdot \dfrac{4}{7} \cdot \dfrac{4}{7} + \dfrac{3}{7} \cdot \dfrac{3}{7} + \dfrac{3}{7}$
$=(4/7)^3+(3/7)^3$
$=\dfrac{13}{40}\approx 27\,\%$
b)
Ahora, hemos de tener en cuenta ( a la hora de asignar probabilidades ) que al no reemplazar las bolas que se van extrayendo, alteramos el contenido de la urna en cada extracción. Así,
$P((B_3 \cap B_2 \cap B_1) \cup (N_3 \cap N_2 \cap N_1))=$
$=P(B_3 | B_2 \cap B_1)\cdot P(B_2 \cap B_1) + P(N_3 | N_2 \cap N_1)\cdot P(N_2 \cap N_1)$
$=P(B_3 | B_2 \cap B_1)\cdot P(B_2|B_1)\cdot P(B_1) + P(N_3 | N_2 \cap N_1)\cdot P(N_2|N_1)\cdot P(N_1)$
$=\dfrac{4}{7} \cdot \dfrac{3}{6} \cdot \dfrac{2}{5} + \dfrac{3}{7} \cdot \dfrac{2}{6} + \dfrac{1}{5}$
$=\dfrac{1}{7} \approx 14\,\%$
$\square$
Ejercicios de combinatoria
a) Formar una comisión de $4$ personas, elegidas entre un grupo que consta de $6$ personas
b) Sentar a $5$ personas en una fila de $5$ butacas numeradas
c) Elaborar banderas de señales de $3$ franjas verticales con $4$ telas de colores, siendo posible repetir los colores en una bandera
d) Escribir "palabras" con las letras de la palabra ELEMENTAL, de modo que en cada palabra aparezca cada una de las letras y con el mismo número de repeticiones que se dan en la palabra de referencia
e) Distribuir $5$ bolas idénticas entre $4$ urnas
SOLUCIÓN.
a)
En este caso no importa el orden en que elegimos a las personas, luego se trata de un cálculo de combinaciones, y, a no poder repetir la elección de una misma persona ( entre el total de seis personas ) para formar un conjunto ( una comisión ) de cuatro personas es un caso de combinaciones ordinarias de $6$ ( personas ) tomadas en conjuntos de cuatro, luego podemos formar la comisión de $C_{6,4}=\dfrac{V_{6,4}}{P_4}=\displaystyle \binom{6}{4}=15$ maneras distintas.
b)
Importa el orden en que colocamos a las personas, luego se trata de un cálculo de variaciones, y, a no poder repetir la elección de una misma persona para completar la fila es un caso de variaciones ordinarias de $5$ ( personas ) tomadas en conjuntos de cinco, luego se podrán sentar de $V_{5,5}=P_{5}=5!=120$ maneras distintas.
c)
Es evidente que el orden de elección de color al llenar las tres franjas ( pongamos que de izquierda a derecha ) es importante para distinguir una señal de otra, luego se trata de un problema de variaciones; como, además, podemos elegir el mismo color en más de una franja, es un problema de variaciones con repetición de $4$ colores tomados en conjuntos de tres, luego podremos representar $VR_{4,3}=4^3=64$ señales distintas.
d)
Este es un problema en que importa el orden, pues dos palabras con las mismas letras ( y apareciendo cada una el mismo número de veces que en la palabra ELEMENTAL: tres Es, dos Ls, una M, una N, una T y una A ) dispuestas en distinto orden tienen significados distintos, luego es un problema de variaciones. Como, en este caso, deben aparecer todas y cada una de las letras y el mismo número de veces que aparece cada una en la palabra de referencia, se trata de un caso de permutaciones con repetición, esto es, el número de palabras que podemos formar es $PR_{9}^{3,2,1,1,1,1}=\dfrac{9!}{3!\cdot 2! \cdot 1! \cdot 1! \cdot 1!\cdot 1! }=30240$
e)
En esta situación no importa el orden en que escogemos las bolas al ir depositándolas en las urnas, pues no nos importa qué bolas hay en cada urna sino el número de bolas que va a contener cada una de las cuatro urnas, por tanto el problema es de combinaciones; además, podemos poner varias bolas en una misma urna, luego hay que contar con las repeticiones a decidir en qué urnas van las bolas, por lo cual clasificamos el problema como un problema de combinaciones con repetición, en el que se han distribuido $5$ objetos idénticos entre $4$ urnas, luego $\text{CR}_{4,5}:=\displaystyle \binom{5+4-1}{4-1}=\binom{5+4-1}{5}=\dfrac{(5+4-1)!}{5!\cdot (4-1)!} = 56$ maneras distintas de colocar las bolas. Nota: también puede designarse de la forma $\displaystyle \left(\binom{4}{5}\right)$.
$\square$
domingo, 12 de junio de 2016
Ejercicios resueltos del examen final del tercer trimestre ( temas 13,14,15 y 16 ), realizado el Jueves 09/06/2016
Segunda parte ( temas 15 y 16 ): [ 3 | 4 ]
Un ejercicio sobre la probabilidad total ( teoremas de la Probabilidad Total y de Bayes )
a) Calcular la probabilidad de que la persona elegida estudie formación profesional
b) Se sabe que la persona elegida estudia formación profesional, ¿ cuál es la probabilidad de que sea chica ?
SOLUCIÓN.
Denotemos ( los sucesos ) por:
$F$: elegir una persona que estudie formación profesional
$M$: elegir una persona que sea chica
$H$: elegir una persona que sea chico
a)
Como $F=(F \cap M) \cup ( F \cap H)$ y los sucesos $F \cap M$ y $F \cap H$ son disjuntos ( incompatibles ), podemos escribir $P(F)=P(F \cap M)+P(F \cap H)$; y, por la definición de probabilidad condicionada, obtenemos lo que se afirma en el teorema de la Probabilidad Total $$P(F)=P(F|M)\cdot P(M)+P(F|H)\cdot P(H)$$ Poniendo ahora los datos del problema $$P(F)=\dfrac{4}{9}\cdot \dfrac{9}{9+7}+\dfrac{3}{7}\cdot \dfrac{7}{9+7}=\dfrac{7}{16}\approx 44\,\%$$
b)
Teniendo en cuenta el teorema de Bayes $$P(M|F)=\dfrac{P(F|M)\cdot P(M)}{P(F)}$$ y con los datos del problema $$P(M|F)=\dfrac{\dfrac{4}{9}\cdot \dfrac{9}{9+7}}{7/16}=\dfrac{4}{7} \approx 57\,\%$$
$\square$
Extracciones de bolas de una urna
a) con reemplazamiento de las bolas que se van sacando
b) sin reemplazamiento
SOLUCIÓN.
Este problema puede abordarse de varias maneras. Aquí, hemos elegido la del cálculo combinatorio. Entendiendo las bolas como distinguibles, aún siendo del mismo color ( podemos imaginar que llevan un número grabado ), el espacio muestral, así pensado, está formado por sucesos elementales, por lo que podemos emplear la regla de Laplace para la asignación de probabilidades.
Denominemos $S$ al suceso "elegir las tres bolas del mismo color". Entonces, por la regla de Laplace, $P(S)=\dfrac{N(S)}{N}$, donde notamos por $N$ el número de casos en total, y por $N(S)$ el número de casos favorables al suceso $S$.
a)
Si las extracciones se realizan con reemplazamiento, $N(S)=VR_{6,3}+VR_{8,3}$; y, $N=VR_{6+8,3}$, luego $$P(S)=\dfrac{VR_{6,3}+VR_{8,3}}{VR_{6+8,3}}=\dfrac{728}{2744}=\dfrac{13}{49} \approx 27\,\%$$
b)
En el caso de que las extracciones sean sin reemplazamiento, es equivalente a pensar que sacamos las tres bolas a la vez. En tal caso, $N(s)=C_{6,3}+ C_{8,3}=\displaystyle \binom{6}{3}+\binom{8}{3}$ y $N=C_{6+8,3}=\displaystyle \binom{14}{3}$, luego $$P(S)=\dfrac{\displaystyle \binom{6}{3}+ \binom{8}{3}}{\displaystyle \binom{14}{3}}=\dfrac{76}{364}=\dfrac{19}{91} \approx 21\,\%$$
$\square$
Un ejercicio de combinatoria
a) Formar una comisión de $3$ personas, elegidas entre un grupo que consta de $5$ personas
b) Sentar a $4$ personas en una fila de $4$ butacas numeradas
c) Elaborar banderas de señales de $3$ franjas verticales con $5$ telas de colores, siendo posible repetir los colores en una bandera
d) Escribir "palabras" con las letras de la palabara CASA, de modo que en cada palabra aparezca cada una de las letras y con el mismo número de repeticiones que se dan en la palabra de referencia
e) Distribuir $5$ lápices ( de distintos colores ) entre $4$ niños
SOLUCIÓN.
a)
En este problema no importa el orden en que colocamos las personas elegidas, y, evidentemente no podemos repetir personas en la elección de las mismas, por lo que identificamos el problema como un problema de combinaciones ordinarias de $5$ ( personas ) tomadas en conjuntos de tres personas: $C_{5,3}=\dfrac{V_{5,3}}{P_3}=\displaystyle \binom{5}{3}=10$
b)
Como es relevante el orden en el que se sientas las personas, se trata de un problema de variaciones; y, al no poder sentar la misma personas en distintos asientos, las variaciones son ordinarias ( sin repetición ), luego podemos distribuirlas en los asientos de $V_{4,4}=P_{4}=4!=24$ maneras distintas.
c)
Aquí también importa el orden, por lo que se trata de un problema de variaciones; sin embargo, sí es posible, ahora, repetir colores en la confección de las tres franjas, por consiguiente el problema es de variaciones con repetición de $5$ colores tomados en conjuntos de tres, y el número de señales que podemos codificar es $VR_{5,3}=5^3=125$.
d)
En todas las palabras que formemos deberá haber las mismas letras y el mismo número de cada una de ellas que en la palabra de referencia CASA. Además, es claro que importa el orden de colocación de las letras, por lo que tenemos un problema de variaciones, y, en particular, de permutaciones con repetición. El número de palabras que podemos formar es $$PR_{4}^{2,1,1}=\dfrac{4!}{2!\cdot 1! \cdot 1!}=12$$
e)
Este problema es análogo al problema de distribuir $5$ bolas que lleven alguna marca que distinga unas de otras ( por lo que se trata de un problema en el que importa el orden ) en $4$ urnas. En otras palabras, queremos encontrar el número de conjuntos de $5$ elementos que podemos formar eligiendo entre $4$ niños; esto es, se trata de un problema de variaciones con repetición, por lo que podemos hacer la distribución pedida de $VR_{4,5}=4^5=1024$ maneras distintas. $\square$
Ejercicios sobre estadística de una variable con datos agrupados en intervalos
SOLUCIÓN.
Histograma de frecuencias absolutas del recuento:
Podemos apreciar ( en el procedimiento gráfico ) que la moda, $M_o$, es aproximadamente igual a $59$
Histograma de frecuencias acumuladas y diagrama de caja:
$\square$
miércoles, 4 de mayo de 2016
Calcular de cuántas maneras es posible ...
a) Constituir una comisión de $4$ personas de entre un grupo de $15$ personals en total
b) Sentar a $5$ personas en una fila de $5$ butacas
c) Elaborar banderas de señales de $4$ franjas con $8$ telas de colores
d) Escribir "palabras" con las letras de PARALELEPÍPEDO
e) Construir números enteros positivos múltiplos de $5$, que sean mayores que $100$ y menores que $500$, con sus tres dígitos distintos.
SOLUCIÓN.
a) En este caso no importa el orden en el que tomamos las cuatro personas, y, por supuesto, no podemos repetir personas en la selección, luego se trata de un caso de combinaciones ordinarias, y el número de posibilidades es $C_{15,4}=\dfrac{V_{15,4}}{P_4}=\dfrac{15\cdot 14 \cdot 13 \cdot 12}{4 \cdot 3 \cdot 2 \cdot 1}=1365$
b) Como hay que tener en cuenta el orden de colocación, se trata de un caso de variaciones; y, además, es claro que no podemos repetir las personas, luego estamos ante un problema de variaciones ordinarias en el que el número de "objetos" ( las personas ) a seleccionar coincide con el tamaño de los grupos que tomamos, lo cual nos lleva ( en particular ) a un problema de permutaciones. El número de posibilidades es $V_{5,5}=P_5=5!=120$
c) Aquí importa también el orden en el tomamos los objetos ( que son los colores ), luego el problema es de variaciones; y como nada nos impide repetir los colores al distribuirlos en las franjas, estamos ante un problema de variaciones con repetición, y el número de posibilidades es $VR_{8,4}=8^4=4096$
e) En este caso importa el orden en el que colocamos las letras ( las "palabras" resultantes no tienen porque tener un significado ); sin embargo, algunas de las letras aparecen repetidas. Y como en cada palabra hay que emplear todas y cada una de ellas, estamos ante un problema de permutaciones con repetición, y el número de posibilidades es $PR_{14}^{3,2,1,2,3,1,1,1}=\dfrac{14!}{3!\cdot 2! \cdot 1! \cdot 2! \cdot 3! \cdot 1! \cdot 1! \cdot 1!}=605\,404\,800$
f)
Procedimiento 1.
Podemos elegir el dígito de las unidades de $2$ maneras, pues sólo puede ser '0' o bien '5' ( por tener que ser los números pedidos múltiplos de cinco ). Por otra parte, podemos elegir el dígito de las centenas entre el '1', el '2', el '3' y el '4' ( así nos aseguramos de que los números que se pueden formar son mayores que cien y menores o iguales que quinientos ), esto es, tenemos $4$ posibilidades para elegir el dígito de las unidades. Además, podremos elegir el dígito de las decenas entre las diez cifras '0', '1', ..., '9', luego tenemos $10$ posibilidades para ello. Aplicando ahora el principio multiplicativo, vemos que hay un total de $4 \cdot 10 \cdot 2 = 80$ números múltiplos de cinco que son mayores que cien y menores o iguales que quinientos. Ahora bien, como se nos pide que dichos números sean, además, menores que quinientos, deberemos restar de la cantidad encontrada el caso que corresponde a formar el número quinientos ( que entra en el cómputo anterior ), luego tendremos un total de $80-1=79$ números múltiplos de cinco, mayores que cien y menores que quinientos.
Procedimiento 2.
El menor múltiplo de $5$ en dicho conjunto es $105$, y el mayor $495$; entonces, como el conjunto de múltiplos están separados por la misma "distancia" ( espacios entre dos múltiplos consecutivos, que es $5$ ), el número de múltiplos pedidos ( mayores que $100$ y menores que $500$ ) es $ \dfrac{495-105}{5}+1=79$
$\square$
jueves, 7 de abril de 2016
lunes, 4 de abril de 2016
Representar la gráfica de la función ...
SOLUCIÓN.
Calculando la imagen de unos cuantos valores de la variable independiente: $-3,-2,-1,0,1,2,3$ y representando los puntos en un diagrama cartesiano:
Se trata de una función exponencial ( $x$ figura en el exponente de la potencia, cuya base es una constante igual a $2$ ) decreciente en todos los puntos ( monótona decreciente ).
$\square$
Hallar la función tal que ...
a) Determinar la expresión ( algebraica ) de la función, $y=f(x)$
b) Calcular la imagen de $3$
c) Calcular la antiimagen de $-2$
SOLUCIÓN.
a)
Una función de proporcionalidad directa ( o lineal afín ) se escribe de la forma $f(x)=m\,x+k$, pues su gráfica es una recta; siendo $m$ la pendiente, y $k$ la ordenada en el origen de la misma. Para encontrar el valor de estos coeficientes, impondremos que los puntos $A(-1,-1)$ y $B(2,5)$ están en dicha recta, por lo cual deberán cumplirse el siguiente sistema de ecuaciones: $$\left\{\begin{matrix}(-1)\cdot m &+& k&=& -1\\2\cdot m &+& k&=& 5\end{matrix}\right.$$ que podemos resolver fácilmente sin más que sumar, miembro a miembro, sendas ecuaciones, obteniendo la ecuación equivalente $$3m=6$$ de la cual deducimos que $m=3$. Sustituyendo dicho valor en cualquier de las dos ecuaciones originales, encontramos el valor de $k$, que resulta ser $k=1$. Así, la ecuación pedida es $$f(x)=2x+1$$
b)
La imagen de $x=3$ es $f(3)=2 \cdot 3+1 = 7$
c)
Dado un punto de ordenada igual a $-2$, podemos escribir que $$-2=2x+1$$ luego, despejando $x$ obtenemos $$x=-\dfrac{3}{2}$$ Por tanto podemos afirmar que la antiimagen de $-2$ ( esto es, $f^{-1}(-2)$ ) es $-\dfrac{3}{2}$
$\square$
Hallar los elementos notables de la función cuadrática ...
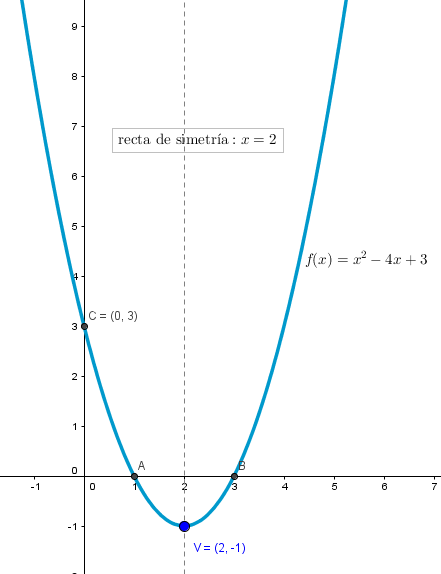
Sea la función $f(x)=x^2-4x+3$. Se pide:
a) Determinar las raíces de dicha función
b) Calcular la ordenada en el origen
c) Calcular las coordenadas del punto de ordenada mínima
d) Representar la gráfica de la función
SOLUCIÓN.
a)
Las raíces de una función polinómica forman el conjunto $\{x\in \mathbb{R}: f(x)=0\}$; imponiendo, pues, la condición $f(x)=0$, vemos que las raíces son las soluciones de la ecuación de segundo grado $x^2-4x+3=0$, por tanto, y teniendo en cuenta que los coeficientes del polinomio del primer miembro son $a=1$, $b=-4$ y $c=3$, encontramos: $$x^2-4x+3=0 \Leftrightarrow x=\dfrac{-(-4)\pm\sqrt{(-4)^2-4\cdot 1 \cdot 3}}{2 \cdot 1}=\left\{\begin{matrix}-3\\\\-1\end{matrix}\right.$$ y por tanto la gráfica de la función corta al eje de abscisas en los puntos $A(3,0)$ y $B(1,0)$
b)
La ordenada en el origen es la imagen de $x=0$: $$f(0)=0^2-4\cdot 0+3=3$$ luego la gráfica de la función corta al eje de ordenadas en el punto $C(0,3)$
c)
La función dada es cuadrática ( polinomio de segundo grado ), luego la gráfica de la función es una parábola, que se abre en el sentido positivo del eje de ordenadas, pues el coeficiente de grado dos es mayor que cero ( $a=1 > 0 $ ); de ahí que nos pidan el punto de ordenada mínima, que no es otro ( en este caso ) que el vértice de la parábola. La abscisa del vértice de una parábola se calcula, en general, mediante la fórmula $x_V=-\dfrac{b}{2a}$ ( tal como se ha justificado en clase ) y, por tanto, poniendo los datos obtenemos $$x_V=-\dfrac{-4}{2\cdot 1}=2$$
Nota 1. También podemos calcularlo, en este caso que la función tiene raíces, de otra forma: a partir de las mismas, basta obtener el punto medio del segmento $AB$, estoe es $x_V=\dfrac{3+1}{2}=2$
La ordenada del vértice ( la ordenada mínima ), $y_V$, es la imagen de $x_V$, luego $$y_V=f(x_V)=f(2)=2^2-4\cdot 2+3=-1$$
Así, pues, el punto de ordenada mínima es $$V(2,-1)$$
Nota 2. Por el vértice de la parábola pasa la recta de simetría, paralela al eje de ordenadas, y que, por tanto, tiene por ecuación: $x=2$
d)
Reuniendo toda la información que hemos encontrado ( elementos notables de la función cuadrática dada ) podemos ya representar su gráfica:
$\square$