Hallar los elementos notables de la función cuadrática ...

ENUNCIADO.
Sea la función $f(x)=x^2-4x+3$. Se pide:
a) Determinar las raíces de dicha función
b) Calcular la ordenada en el origen
c) Calcular las coordenadas del punto de ordenada mínima
d) Representar la gráfica de la función

SOLUCIÓN.
a)
Las raíces de una función polinómica forman el conjunto $\{x\in \mathbb{R}: f(x)=0\}$; imponiendo, pues, la condición $f(x)=0$, vemos que las raíces son las soluciones de la ecuación de segundo grado $x^2-4x+3=0$, por tanto, y teniendo en cuenta que los coeficientes del polinomio del primer miembro son $a=1$, $b=-4$ y $c=3$, encontramos: $$x^2-4x+3=0 \Leftrightarrow x=\dfrac{-(-4)\pm\sqrt{(-4)^2-4\cdot 1 \cdot 3}}{2 \cdot 1}=\left\{\begin{matrix}-3\\\\-1\end{matrix}\right.$$ y por tanto la gráfica de la función corta al eje de abscisas en los puntos $A(3,0)$ y $B(1,0)$

b)
La ordenada en el origen es la imagen de $x=0$: $$f(0)=0^2-4\cdot 0+3=3$$ luego la gráfica de la función corta al eje de ordenadas en el punto $C(0,3)$

c)
La función dada es cuadrática ( polinomio de segundo grado ), luego la gráfica de la función es una parábola, que se abre en el sentido positivo del eje de ordenadas, pues el coeficiente de grado dos es mayor que cero ( $a=1 > 0 $ ); de ahí que nos pidan el punto de ordenada mínima, que no es otro ( en este caso ) que el vértice de la parábola. La abscisa del vértice de una parábola se calcula, en general, mediante la fórmula $x_V=-\dfrac{b}{2a}$ ( tal como se ha justificado en clase ) y, por tanto, poniendo los datos obtenemos $$x_V=-\dfrac{-4}{2\cdot 1}=2$$


Nota 1. También podemos calcularlo, en este caso que la función tiene raíces, de otra forma: a partir de las mismas, basta obtener el punto medio del segmento $AB$, estoe es $x_V=\dfrac{3+1}{2}=2$

La ordenada del vértice ( la ordenada mínima ), $y_V$, es la imagen de $x_V$, luego $$y_V=f(x_V)=f(2)=2^2-4\cdot 2+3=-1$$
Así, pues, el punto de ordenada mínima es $$V(2,-1)$$


Nota 2. Por el vértice de la parábola pasa la recta de simetría, paralela al eje de ordenadas, y que, por tanto, tiene por ecuación: $x=2$


d)
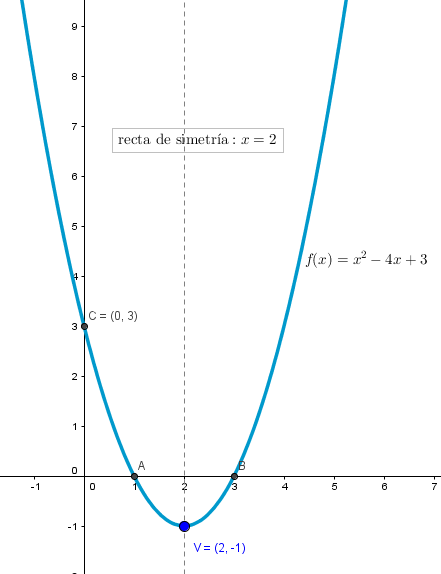
Reuniendo toda la información que hemos encontrado ( elementos notables de la función cuadrática dada ) podemos ya representar su gráfica:

$\square$