jueves, 7 de abril de 2016
lunes, 4 de abril de 2016
Representar la gráfica de la función ...
ENUNCIADO. Representar la gráfica de la función $f(x)=2^{-x}$. ¿ Qué tipo de función es ?.
SOLUCIÓN.
Calculando la imagen de unos cuantos valores de la variable independiente: $-3,-2,-1,0,1,2,3$ y representando los puntos en un diagrama cartesiano:
Se trata de una función exponencial ( $x$ figura en el exponente de la potencia, cuya base es una constante igual a $2$ ) decreciente en todos los puntos ( monótona decreciente ).
$\square$
SOLUCIÓN.
Calculando la imagen de unos cuantos valores de la variable independiente: $-3,-2,-1,0,1,2,3$ y representando los puntos en un diagrama cartesiano:
Se trata de una función exponencial ( $x$ figura en el exponente de la potencia, cuya base es una constante igual a $2$ ) decreciente en todos los puntos ( monótona decreciente ).
$\square$
Hallar la función tal que ...
ENUNCIADO. Considerar una función de proporcionalidad directa, $f(x)$, tal que la gráfica de la misma pasa por los puntos $A(-1,-1)$ y $B(2,5)$. Se pide:
a) Determinar la expresión ( algebraica ) de la función, $y=f(x)$
b) Calcular la imagen de $3$
c) Calcular la antiimagen de $-2$
SOLUCIÓN.
a)
Una función de proporcionalidad directa ( o lineal afín ) se escribe de la forma $f(x)=m\,x+k$, pues su gráfica es una recta; siendo $m$ la pendiente, y $k$ la ordenada en el origen de la misma. Para encontrar el valor de estos coeficientes, impondremos que los puntos $A(-1,-1)$ y $B(2,5)$ están en dicha recta, por lo cual deberán cumplirse el siguiente sistema de ecuaciones: $$\left\{\begin{matrix}(-1)\cdot m &+& k&=& -1\\2\cdot m &+& k&=& 5\end{matrix}\right.$$ que podemos resolver fácilmente sin más que sumar, miembro a miembro, sendas ecuaciones, obteniendo la ecuación equivalente $$3m=6$$ de la cual deducimos que $m=3$. Sustituyendo dicho valor en cualquier de las dos ecuaciones originales, encontramos el valor de $k$, que resulta ser $k=1$. Así, la ecuación pedida es $$f(x)=2x+1$$
b)
La imagen de $x=3$ es $f(3)=2 \cdot 3+1 = 7$
c)
Dado un punto de ordenada igual a $-2$, podemos escribir que $$-2=2x+1$$ luego, despejando $x$ obtenemos $$x=-\dfrac{3}{2}$$ Por tanto podemos afirmar que la antiimagen de $-2$ ( esto es, $f^{-1}(-2)$ ) es $-\dfrac{3}{2}$
$\square$
a) Determinar la expresión ( algebraica ) de la función, $y=f(x)$
b) Calcular la imagen de $3$
c) Calcular la antiimagen de $-2$
SOLUCIÓN.
a)
Una función de proporcionalidad directa ( o lineal afín ) se escribe de la forma $f(x)=m\,x+k$, pues su gráfica es una recta; siendo $m$ la pendiente, y $k$ la ordenada en el origen de la misma. Para encontrar el valor de estos coeficientes, impondremos que los puntos $A(-1,-1)$ y $B(2,5)$ están en dicha recta, por lo cual deberán cumplirse el siguiente sistema de ecuaciones: $$\left\{\begin{matrix}(-1)\cdot m &+& k&=& -1\\2\cdot m &+& k&=& 5\end{matrix}\right.$$ que podemos resolver fácilmente sin más que sumar, miembro a miembro, sendas ecuaciones, obteniendo la ecuación equivalente $$3m=6$$ de la cual deducimos que $m=3$. Sustituyendo dicho valor en cualquier de las dos ecuaciones originales, encontramos el valor de $k$, que resulta ser $k=1$. Así, la ecuación pedida es $$f(x)=2x+1$$
b)
La imagen de $x=3$ es $f(3)=2 \cdot 3+1 = 7$
c)
Dado un punto de ordenada igual a $-2$, podemos escribir que $$-2=2x+1$$ luego, despejando $x$ obtenemos $$x=-\dfrac{3}{2}$$ Por tanto podemos afirmar que la antiimagen de $-2$ ( esto es, $f^{-1}(-2)$ ) es $-\dfrac{3}{2}$
$\square$
Hallar los elementos notables de la función cuadrática ...
ENUNCIADO.
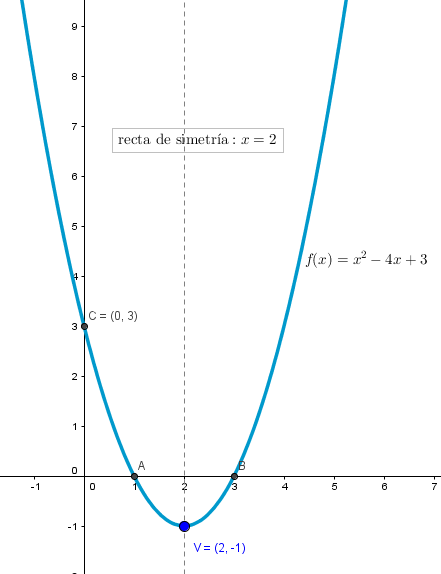
Sea la función $f(x)=x^2-4x+3$. Se pide:
a) Determinar las raíces de dicha función
b) Calcular la ordenada en el origen
c) Calcular las coordenadas del punto de ordenada mínima
d) Representar la gráfica de la función
SOLUCIÓN.
a)
Las raíces de una función polinómica forman el conjunto $\{x\in \mathbb{R}: f(x)=0\}$; imponiendo, pues, la condición $f(x)=0$, vemos que las raíces son las soluciones de la ecuación de segundo grado $x^2-4x+3=0$, por tanto, y teniendo en cuenta que los coeficientes del polinomio del primer miembro son $a=1$, $b=-4$ y $c=3$, encontramos: $$x^2-4x+3=0 \Leftrightarrow x=\dfrac{-(-4)\pm\sqrt{(-4)^2-4\cdot 1 \cdot 3}}{2 \cdot 1}=\left\{\begin{matrix}-3\\\\-1\end{matrix}\right.$$ y por tanto la gráfica de la función corta al eje de abscisas en los puntos $A(3,0)$ y $B(1,0)$
b)
La ordenada en el origen es la imagen de $x=0$: $$f(0)=0^2-4\cdot 0+3=3$$ luego la gráfica de la función corta al eje de ordenadas en el punto $C(0,3)$
c)
La función dada es cuadrática ( polinomio de segundo grado ), luego la gráfica de la función es una parábola, que se abre en el sentido positivo del eje de ordenadas, pues el coeficiente de grado dos es mayor que cero ( $a=1 > 0 $ ); de ahí que nos pidan el punto de ordenada mínima, que no es otro ( en este caso ) que el vértice de la parábola. La abscisa del vértice de una parábola se calcula, en general, mediante la fórmula $x_V=-\dfrac{b}{2a}$ ( tal como se ha justificado en clase ) y, por tanto, poniendo los datos obtenemos $$x_V=-\dfrac{-4}{2\cdot 1}=2$$
Nota 1. También podemos calcularlo, en este caso que la función tiene raíces, de otra forma: a partir de las mismas, basta obtener el punto medio del segmento $AB$, estoe es $x_V=\dfrac{3+1}{2}=2$
La ordenada del vértice ( la ordenada mínima ), $y_V$, es la imagen de $x_V$, luego $$y_V=f(x_V)=f(2)=2^2-4\cdot 2+3=-1$$
Así, pues, el punto de ordenada mínima es $$V(2,-1)$$
Nota 2. Por el vértice de la parábola pasa la recta de simetría, paralela al eje de ordenadas, y que, por tanto, tiene por ecuación: $x=2$
d)
Reuniendo toda la información que hemos encontrado ( elementos notables de la función cuadrática dada ) podemos ya representar su gráfica:
$\square$
Sea la función $f(x)=x^2-4x+3$. Se pide:
a) Determinar las raíces de dicha función
b) Calcular la ordenada en el origen
c) Calcular las coordenadas del punto de ordenada mínima
d) Representar la gráfica de la función
SOLUCIÓN.
a)
Las raíces de una función polinómica forman el conjunto $\{x\in \mathbb{R}: f(x)=0\}$; imponiendo, pues, la condición $f(x)=0$, vemos que las raíces son las soluciones de la ecuación de segundo grado $x^2-4x+3=0$, por tanto, y teniendo en cuenta que los coeficientes del polinomio del primer miembro son $a=1$, $b=-4$ y $c=3$, encontramos: $$x^2-4x+3=0 \Leftrightarrow x=\dfrac{-(-4)\pm\sqrt{(-4)^2-4\cdot 1 \cdot 3}}{2 \cdot 1}=\left\{\begin{matrix}-3\\\\-1\end{matrix}\right.$$ y por tanto la gráfica de la función corta al eje de abscisas en los puntos $A(3,0)$ y $B(1,0)$
b)
La ordenada en el origen es la imagen de $x=0$: $$f(0)=0^2-4\cdot 0+3=3$$ luego la gráfica de la función corta al eje de ordenadas en el punto $C(0,3)$
c)
La función dada es cuadrática ( polinomio de segundo grado ), luego la gráfica de la función es una parábola, que se abre en el sentido positivo del eje de ordenadas, pues el coeficiente de grado dos es mayor que cero ( $a=1 > 0 $ ); de ahí que nos pidan el punto de ordenada mínima, que no es otro ( en este caso ) que el vértice de la parábola. La abscisa del vértice de una parábola se calcula, en general, mediante la fórmula $x_V=-\dfrac{b}{2a}$ ( tal como se ha justificado en clase ) y, por tanto, poniendo los datos obtenemos $$x_V=-\dfrac{-4}{2\cdot 1}=2$$
Nota 1. También podemos calcularlo, en este caso que la función tiene raíces, de otra forma: a partir de las mismas, basta obtener el punto medio del segmento $AB$, estoe es $x_V=\dfrac{3+1}{2}=2$
La ordenada del vértice ( la ordenada mínima ), $y_V$, es la imagen de $x_V$, luego $$y_V=f(x_V)=f(2)=2^2-4\cdot 2+3=-1$$
Así, pues, el punto de ordenada mínima es $$V(2,-1)$$
Nota 2. Por el vértice de la parábola pasa la recta de simetría, paralela al eje de ordenadas, y que, por tanto, tiene por ecuación: $x=2$
d)
Reuniendo toda la información que hemos encontrado ( elementos notables de la función cuadrática dada ) podemos ya representar su gráfica:
$\square$
Calcular la capacidad de un depósito que tiene forma de tronco de cono
ENUNCIADO. Calcular la capacidad ( en litros ) de un depósito de agua que tiene la forma de un tronco de cono, cuyas bases tienen radios de $3$ y $6$ metros, respectivamente; siendo la longitud de la generatriz de dicho tronco de cono igual a $5$ metros.
ENUNCIADO.
El volumen de un tronco de cono de radios $r_1$ y $r_2$ y altura $h$ viene dado por la fórmula ( justificada en clase ) $$V=\dfrac{h\,\pi}{3}\,(r_{1}^2+r_{2}^2+r_1\,r_2)$$
Para aplicarla, necesitamos antes calcular el valor de $h$, a partir de $r_1$, $r_2$ y $g$. Dibujando la figura, podemos observar ( en la sección diametral ) que se forma un triángulo rectángulo cuya hipotenusa es $g$ y de catetos $r_1-r_2$ ( siendo $r_1 > r_2 )$ y $h$, por lo que podemos aplicar el teorema de Pitágoras para determinar $h$: $$h=\sqrt{g^2-(r_1-r_2)^2}=\sqrt{5^2-(6-3)^2}=\sqrt{5^2-3^2}=\sqrt{16}=4 \; \text{m}$$
Entonces, de la expresión del volumen obtenemos $$V=\dfrac{4\,\pi}{3}\,(3^2+6^2+3 \cdot 6)=84\,\pi\;\text{m}^3$$ Finalmente, obtenemos la capacidad pedida, $C$, teniendo en cuenta que $1\; \text{m^3}$ equivale a $1000\,\text{L}$; por consiguiente $$C=84\,000\,\pi\; \text{L} \approx 263\,893 \; \text{L}\;\; \text{(aproximando por defecto a las unidades)}$$
$\square$
ENUNCIADO.
El volumen de un tronco de cono de radios $r_1$ y $r_2$ y altura $h$ viene dado por la fórmula ( justificada en clase ) $$V=\dfrac{h\,\pi}{3}\,(r_{1}^2+r_{2}^2+r_1\,r_2)$$
Para aplicarla, necesitamos antes calcular el valor de $h$, a partir de $r_1$, $r_2$ y $g$. Dibujando la figura, podemos observar ( en la sección diametral ) que se forma un triángulo rectángulo cuya hipotenusa es $g$ y de catetos $r_1-r_2$ ( siendo $r_1 > r_2 )$ y $h$, por lo que podemos aplicar el teorema de Pitágoras para determinar $h$: $$h=\sqrt{g^2-(r_1-r_2)^2}=\sqrt{5^2-(6-3)^2}=\sqrt{5^2-3^2}=\sqrt{16}=4 \; \text{m}$$
Entonces, de la expresión del volumen obtenemos $$V=\dfrac{4\,\pi}{3}\,(3^2+6^2+3 \cdot 6)=84\,\pi\;\text{m}^3$$ Finalmente, obtenemos la capacidad pedida, $C$, teniendo en cuenta que $1\; \text{m^3}$ equivale a $1000\,\text{L}$; por consiguiente $$C=84\,000\,\pi\; \text{L} \approx 263\,893 \; \text{L}\;\; \text{(aproximando por defecto a las unidades)}$$
$\square$
Calcular la altura de un árbol que visto desde un ángulo de ...
ENUNCIADO. Calcular la altura de un árbol ( que se eleva perpendicular al suelo horizontal ) sabiendo que el ángulo que forma la visual trazada desde el punto más alto al suelo es de $60^{\circ}$, y que la distancia entre el pie del árbol y el observador ( que tiene una estatura de $1,7$ metros y está observando de pie ) es de $15,7$ metros.
SOLUCIÓN.
Dada la situación, podemos configurar un triángulo rectángulo con el segmento de la recta visual cuyos extremos son el punto más alto del árbol y el ojo del observador, el segmento horizontal del pie del observador al pie del árbol, y la parte del árbol ( perpendicular al suelo ), $x$, comprendida entre su punto más alto y un punto situado a la misma altura que el ojo del observador. Entonces, por la definición de la razón tangente del ángulo que forma la visual con el plano horizontal, podemos escribir $$\tan\,60^{\circ}=\dfrac{x}{15,72}$$ y despejando $x$ $$x=15,72 \cdot \tan\,60^{\circ}=15,7\cdot \sqrt{3}\; \text{m}$$ Para acabar de calcular la altura del árbol, $h$, deberemos sumarle el tramo que corresponde a la altura del ojo del observador, que es $1,70\; \text{m}$, así: $$h=x+1,70 \approx 15,7\cdot \sqrt{3}+1,7 \approx 28,9 \; \text{m}$$
$\square$
SOLUCIÓN.
Dada la situación, podemos configurar un triángulo rectángulo con el segmento de la recta visual cuyos extremos son el punto más alto del árbol y el ojo del observador, el segmento horizontal del pie del observador al pie del árbol, y la parte del árbol ( perpendicular al suelo ), $x$, comprendida entre su punto más alto y un punto situado a la misma altura que el ojo del observador. Entonces, por la definición de la razón tangente del ángulo que forma la visual con el plano horizontal, podemos escribir $$\tan\,60^{\circ}=\dfrac{x}{15,72}$$ y despejando $x$ $$x=15,72 \cdot \tan\,60^{\circ}=15,7\cdot \sqrt{3}\; \text{m}$$ Para acabar de calcular la altura del árbol, $h$, deberemos sumarle el tramo que corresponde a la altura del ojo del observador, que es $1,70\; \text{m}$, así: $$h=x+1,70 \approx 15,7\cdot \sqrt{3}+1,7 \approx 28,9 \; \text{m}$$
$\square$
Suscribirse a:
Entradas (Atom)